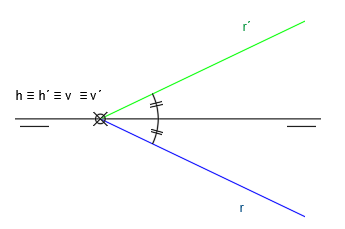
Recuerda que si un punto pertenece al primer bisector, tendrá igual cota que alejamiento. La LT se convierte en un eje de simetría.

Por tanto, si una recta está contenida en el 1er Bisector, sus puntos tendrán igual cota que alejamiento. Por ello, la LT se convierte en la bisectriz que forman el ángulo entre la proyección vertical y horizontal o lo que es lo mismo, el ángulo entre la proyección vertical y la LT es el mismo que entre esta y la proyección horizontal.

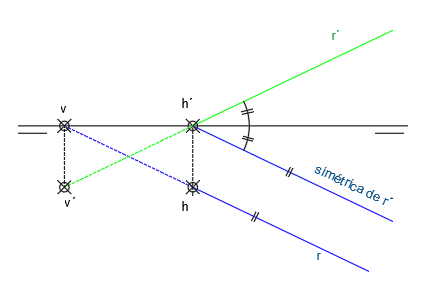
Una recta paralela al 1er bisector nunca lo cortará. Por tanto, si la simétrica de r´es paralela a r, dicha recta será paralela al primer bisector.

Para averiguar si una recta es paralela al 1er bisector, trazaremos la simétrica de r´usando como eje de simetría la LT. Replicaremos el ángulo formado entre r´y la LT. Si dicha nueva recta es paralela a r, dicha recta será paralela al 1er bisector.

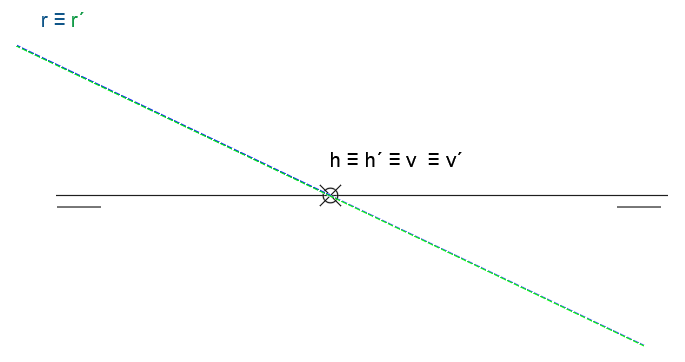
Recuerda que si un punto pertenece al 2º bisector, sus proyecciones coinciden. Por tanto, si una recta pertenece al 2º bisector, sus dos proyecciones también coincidirán en sí mismas. Siempre se verán como una línea recta, tal como tienes de ejemplo en el dibujo.

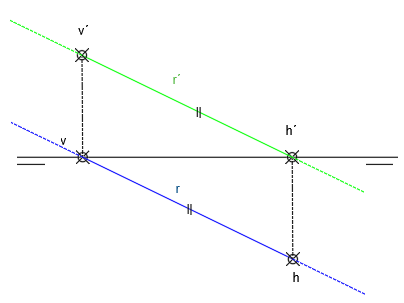
Una recta paralela al 2º bisector nunca lo cortará. Por tanto, las proyecciones horizontales y verticales de la recta, no podrán cortarse.

Para averiguar si una recta es paralela al 2º bisector, solo tendremos que analizar, si r´y r son paralelas. Si lo son, será paralela al 2º bisector.