Elipse

1- ¿Por qué es importante el estudio de la elipse?

Es importante por varias razones:

1. La elipse es una de las curvas cónicas y, por lo tanto, está relacionada con el cono, que es una figura geométrica fundamental en la geometría. El estudio de la elipse y de otras curvas cónicas ha sido fundamental en la historia de las matemáticas y ha tenido importantes aplicaciones en diversas ramas de la ciencia, como la óptica, la física, la ingeniería y la astronomía.
2. La elipse es una figura geométrica muy común en la vida cotidiana, ya que muchas formas de la naturaleza y de la tecnología tienen una forma elíptica. Por ejemplo, las órbitas de los planetas alrededor del sol son elípticas, las ruedas de los vehículos pueden ser elípticas y muchas herramientas y objetos tienen formas elípticas. Por lo tanto, el estudio de la elipse nos ayuda a entender mejor el mundo que nos rodea.
3. La elipse tiene propiedades matemáticas interesantes y útiles. Por ejemplo, la elipse tiene dos focos, y la suma de las distancias desde cualquier punto de la elipse a los dos focos es constante. Esta propiedad se utiliza en muchas aplicaciones prácticas, como en la construcción de telescopios y en la transmisión de señales de radio.
4. El estudio de la elipse puede ser beneficioso para el desarrollo de habilidades matemáticas y la capacidad de razonamiento lógico. La resolución de problemas relacionados con la elipse puede ayudar a mejorar la comprensión de conceptos matemáticos y a desarrollar habilidades analíticas y de pensamiento crítico.

2- Qué es una elipse.

La elipse es el lugar geométrico de los puntos de la curva que cumplen la condición de que la suma de distancias de cualquiera de ellos a otros dos fijos, denominados focos, es constante. En el siguiente video te explico esta definición, así como las propiedades de esta curva. Si atiendes a esta explicación, podrás realizar a partir de aquí todos los ejercicios posibles con la elipse. Por tanto, te sugiero que imprimas la elipse que te dejo más abajo y dibujes conmigo. Te aseguro que si lo haces, podrás realizar cualquier problema de elipses que se te ponga por delante:

3- ¿Qué son los focos de la elipse y de donde surgen?

Aquí tienes el teorema de Dandelin (que ya viste en la explicación general de las curvas cónicas) aplicado a la elipse. Observando este dibujo, podrás entender de donde salen los diferentes elementos que componen la elipse: focos, directrices y ejes.

La elipse posee dos ejes:

• El eje mayor es considerado el real (AB).
• El menor (CD) es el imaginario o virtual.

Ambos se cortan perpendicularmente en el centro de la elipse y es simétrica respecto de los dos.

Los elementos de esta curva cónica son:

• Focos F, F´: puntos de tangencia del plano secante con las esferas inscritas. Los segmentos que unen un punto de la elipse con ambos focos se denominan radios vectores.
• Directrices (D): son perpendiculares al eje mayor y polares de los focos.
• Excentricidad: varía de 0 a 1. Para entenderla habría que tener en cuenta la siguiente razón: e = 2c/ 2a = c/ a . Sería una razón entre la distancia focal (distancia entre los dos focos FF´) y el eje mayor. La elipse es más achatada cuanto mayor es su excentricidad. Si c, distancia entre los focos, fuese 0 la elipse se transformaría en una circunferencia de centro 0 y radio a. Si c = a los focos coincidirían con los vértices (A,B) el valor de la excentricidad sería 1.
• Parámetros:
  • Eje mayor o real: AB = 2a
  • Eje menor o imaginario: CD = 2b
  • Distancia focal FF´: 2c
  • Entre ellos se cumple: a² = b ² + c² lo cual permite que podamos hallar los focos conociendo los semiejes.

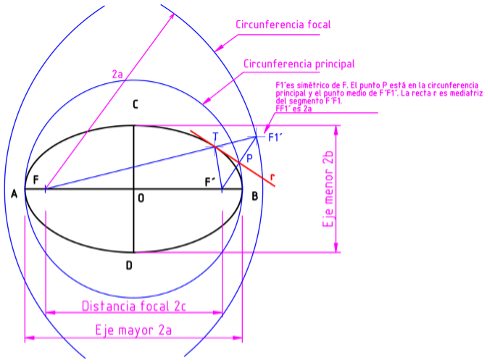
• Circunferencia principal: es la circunferencia con centro en el centro de la elipse y radio a (mitad del eje mayor).
• Circunferencia focal: es aquella cuyo centro está en F o F´ y radio 2a. Es considerada el lugar geométrico de los simétricos de los focos respecto de las tangentes a la elipse.
• Diámetros conjugados: par de diámetros que cumplen la condición de que cualquier recta secante paralela a uno de los diámetros queda dividida en dos partes iguales por el otro diámetro.

¿Preparado para realizar ejercicios sobre la elipse? Aquí puedes descargártelos:

Te dejo algunos videos con la solución a algunos de estos ejercicios:

Para profundizar en este tema, te dejo aquí cómo hallar la intersección de una recta con una elipse sin hacer el trazado de la curva:

A continuación puedes ver la solución a los ejercicios en formato PDF:

En este video tienes cómo resolver la construcción de la elipse por el método de la tarjeta:

Sigue estudiando el resto de curvas cónicas: