Hipérbola

1- ¿Por qué es importante estudiar la hipérbola?

El estudio de la hipérbola en el dibujo técnico es importante debido a su amplio uso en diferentes áreas, como la representación de piezas mecánicas, el diseño de objetos y la arquitectura, así como su relevancia en el cálculo de áreas y volúmenes.

A continuación, se presentan algunas razones por las cuales es importante estudiarla:

1. Representación de piezas mecánicas: La hipérbola es comúnmente utilizada en la representación de piezas mecánicas, como engranajes y levas, debido a sus propiedades geométricas. El conocimiento de cómo dibujar hipérbolas es necesario para poder crear dibujos técnicos precisos de estas piezas.
2. Diseño de objetos: En el diseño de objetos, la hipérbola es una curva que puede ser utilizada para crear formas interesantes y atractivas. Conocer cómo dibujar hipérbolas puede permitir al dibujante crear objetos con formas únicas y atractivas.
3. Arquitectura: La hipérbola también puede ser utilizada en la arquitectura para crear diseños y detalles decorativos. Por ejemplo, las columnas hipérbolicas son una característica común en la arquitectura neoclásica.
4. Cálculo de áreas y volúmenes: El conocimiento de la hipérbola también puede ser útil en el cálculo de áreas y volúmenes. Por ejemplo, la fórmula para calcular el área de una sección transversal de un cono que se corta con un plano inclinado es una hipérbola, y conocer cómo dibujarla correctamente es importante para poder aplicar esta fórmula de manera correcta.

2- Qué es una hipérbola.

La hipérbola es el lugar geométrico de los puntos que cumplen la condición de que la diferencia de distancias a otros dos fijos, llamados focos, es constante e igual a 2ª, eje mayor AB. La hipérbola es una curva abierta, al contrario de la elipse que era cerrada, y posee dos ramas.

Elementos de la hipérbola:

• Focos F, F´: puntos de tangencia del plano secante con las esferas inscritas.
• Directrices: son perpendiculares a los ejes mayores y polares de los focos.
• Excentricidad: tiene como valor c/a. Si c = a los focos coincidirían con los vértices por lo que su excentricidad sería 1. Si a = 0 entonces los vértices coincidirían con el centro O y su excentricidad tendería al infinito. Su excentricidad suele ser mayor que 1. Por todo ello, podemos decir que si la hipérbola se va acercando al eje mayor, su excentricidad disminuye.
• Parámetros:
  • Eje mayor o real: AB = 2a
  • Eje menor o imaginario: CD = 2b
  • Distancia focal FF´: 2c
  • Entre ellos se establece la relación a² = c ² – b² lo cual permite que podamos hallar los focos conociendo los semiejes.
• Circunferencia principal: es la que tiene como diámetro AB y centro en O. Lugar geométrico de los pies de las perpendiculares trazadas desde los focos a cada una de las tangentes a la curva.
• Circunferencia focal: son aquellas circunferencias con radio 2a trazadas desde F y F´. Lugar geométrico de los simétricos de los focos respecto de las tangentes a la curva.
• Asíntotas: son dos rectas que se cortan en el centro de la hipérbola y serían tangentes a ella en el infinito. Se llama hipérbola equilátera a aquella cuyas asíntotas forman 45º con los ejes. Trataremos este concepto con más detalles en un apartado posterior.

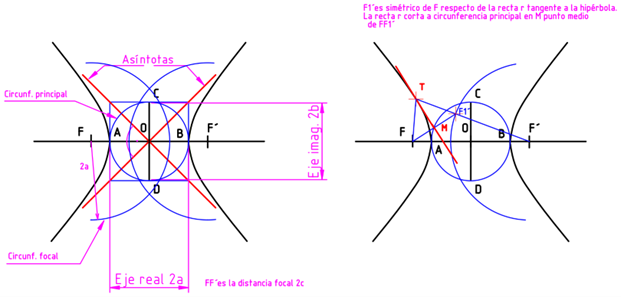
Si atiendes a esta explicación, podrás realizar a partir de aquí todos los ejercicios posibles con la hipérbola. En consecuencia, te sugiero que imprimas la lámina de la hipérbola que te dejo más abajo y dibujes conmigo. Te aseguro que si lo haces, podrás realizar cualquier problema de hipérbolas que se te ponga por delante:

Imprime esta lámina y dibuja conmigo a la vez que ves el video:

3- ¿Qué son los focos de la hipérbola y de donde surgen?

Aquí tienes el teorema de Dandelin (que ya viste en la explicación general de las curvas cónicas) aplicado a la parábola. Observando este dibujo, podrás entender de donde salen los diferentes elementos que componen la elipse: focos, directrices y ejes.

¿Preparado para realizar ejercicios sobre la hipérbola? Aquí puedes descargártelos:

Un ejercicio de selectividad sobre hipérobolas:

Solución en video:

Su solución gráfica:

Sigue estudiando el resto de curvas cónicas: