Circunferencias coaxiales.
Son aquellas circunferencias que tienen un eje radical común. Todas ellas forman un haz, y sus centros están situados en una recta perpendicular a su eje radical.
En la siguiente animación puedes ver como todas las circunferencias que pasan por los puntos dados P y Q, tienen sus centros dispuestos en la mediatriz del segmento PQ, siendo este la secante común a todas las circunferencias coaxiales.
Observa cómo todos los segmentos tangentes a dichas circunferencias, trazadas desde un punto arbitrario (A) tienen la misma longitud, lo que significa que la potencia es la misma.
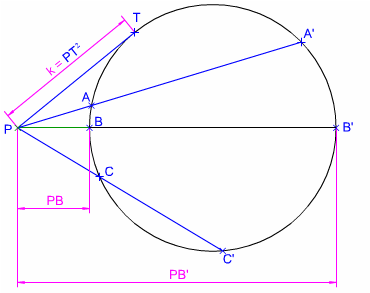
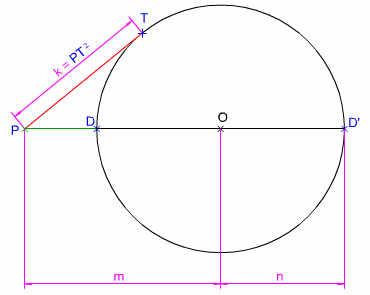 También se puede determinar la potencia considerando el radio de la circunferencia y la distancia del punto exterior al centro.
También se puede determinar la potencia considerando el radio de la circunferencia y la distancia del punto exterior al centro.