Definición.
Se denomina eje radical de dos circunferencias de centros O1 y O2 al lugar geométrico de los puntos del plano que tienen igual potencia respecto de ambas circunferencias
Definición.
Se denomina eje radical de dos circunferencias de centros O1 y O2 al lugar geométrico de los puntos del plano que tienen igual potencia respecto de ambas circunferencias
Eje radical de dos circunferencias.
Para poder determinar el eje radical de dos circunferencias primero tenemos que analizar las distintas posiciones que pueden ocupar en el plano: secantes, tangentes y exteriores.
En la siguiente animación puedes cómo queda dispuesto el eje radical de dos circunferencias según estén dispuestas.
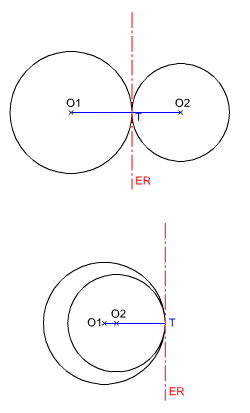 Como vimos en el apartado anterior el eje radical de dos circunferencias tangentes es la recta perpendicular al segmento que une los centros, por su punto de tangencia.
Como vimos en el apartado anterior el eje radical de dos circunferencias tangentes es la recta perpendicular al segmento que une los centros, por su punto de tangencia.
En la imagen de la izquierda tienes dos ejemplos de eje radical de dos circunferencias tangentes (exterior e interior).
Si observas detenidamente la figura inferior (tangentes interiores) puedes ver cómo el eje radical es en realidad la recta tangente a ambas circunferencias.
Determinar el eje radical de dos circunferencias exteriores
Rectas tangentes trazadas desde el eje radical.
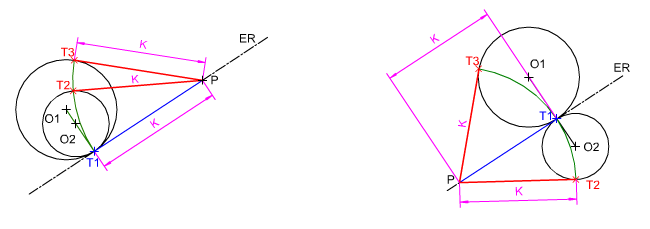
Por tanto, en el caso de circunferencias tangentes entre sí (interiores o exteriores), se tendrá que verificar que los segmentos tangentes (PT), trazados desde cualquier punto P del eje radical, son iguales.
En la animación inferior puedes ver cómo se trazan recta tangentes a dos circunferencias tangentes entre sí (interiores y exteriores) desde un punto situado en el eje radical de dichas circunferencias.
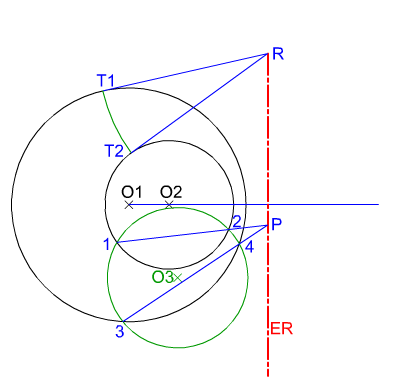 |
Determinar el eje radical de dos circunferencias interiores.
Material necesario:
|
| Para realizar este ejercicio debes descargar este documento pdf. |