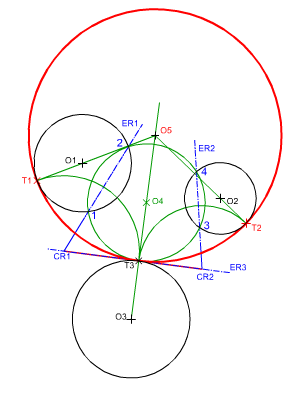
Trazado del ovoide mediante potencia
 El curso anterior aprendimos a trazar ovoide conocidos el eje de simetría, el diámetro mayor y el arco del radio menor mediante un procedimiento complejo, en este enlace puedes repasarlo.
El curso anterior aprendimos a trazar ovoide conocidos el eje de simetría, el diámetro mayor y el arco del radio menor mediante un procedimiento complejo, en este enlace puedes repasarlo.
Para simplificar el trazado puedes aplicar potencia en su resolución.
Como el ovoide está formado por cuatro curvas tangentes interiores, uno de los ejes radicales debe de pasar por la semicircunferencia, perpendicular a su diámetro, el otro se determina mediante una circunferencia auxiliar.
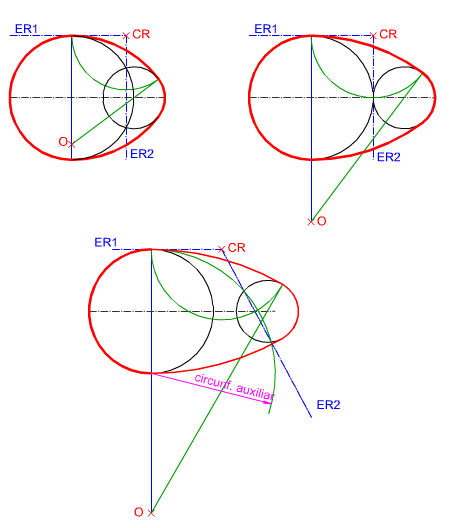
Dependiendo de cómo estén dispuestos los datos (semicircunferencia y arco menor) tendremos tres tipos de ovoide.
- La circunferencia mayor es secante al arco menor: el centro radical queda determinado mediante la intersección de la recta tangente a la semicircunferencia (ER1) y la recta que pasa por los puntos intersección entre ambos arcos (ER2).
- La circunferencia mayor y el arco menor son tangentes: el centro radical queda determinado mediante la intersección de la recta tangente a la semicircunferencia (ER1) y la recta tangente a ambos arcos (ER2).
- La circunferencia mayor es secante al arco menor: el centro radical queda determinado mediante la intersección de la recta tangente a la semicircunferencia (ER1) y el eje radical (ER2) determinado por una circunferencia auxiliar.
En la imagen de la izquierda puedes ver los tres casos anteriormente mencionados.
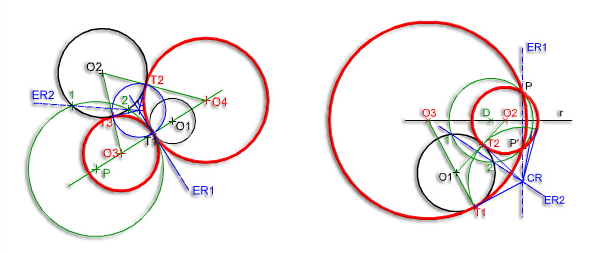
 El curso anterior aprendimos a trazar ovoide conocidos el eje de simetría, el diámetro mayor y el arco del radio menor mediante un procedimiento complejo, en
El curso anterior aprendimos a trazar ovoide conocidos el eje de simetría, el diámetro mayor y el arco del radio menor mediante un procedimiento complejo, en