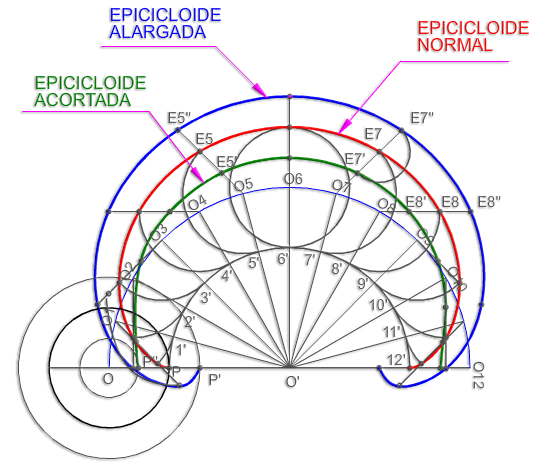
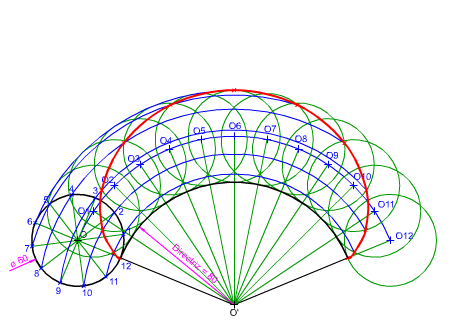
Otras epicicloides.
En una epicicloide el radio de la circunferencia ruleta debe de ser, generalmente, menor que el radio de la circunferencia directriz; sin embargo, la proporción entre ambos radios pueden variar, dando lugar a tres casos particulares:
- Cardioide: el radio de la ruleta es igual al de la circunferencia directriz.
- Lumaca de Pascal: el radio de la ruleta es mayor al de la circunferencia directriz.
- Neforide: el radio de la ruleta es igual a la mitad de la circunferencia directriz.
En la animación inferior puedes ver cómo se genera una cardioide (del griego kardia = corazón y eidos = forma), los puntos de la curva se han obtenido dividiendo la circunferencia directriz en ocho (8) partes iguales.