1.3. Intersección, propiedades
Actividad
Como ya vimos en el apartado 1.1 para resolver la intersección de una recta con una curva cónica debemos aplicar potencia, ya que el punto intersección es el centro de una circunferencia tangente a la focal o directriz pasando siempre por un foco.
En este apartado solamente vamos a estudiar los conceptos que debemos aplicar para resolver los problemas que se plateen más adelante.
Repasa las nuevas definiciones de las curvas cónicas estudiadas en el apartado 1.1.
ELIPSE.
Mediante los conceptos de tangencia y potencia determinamos el centro de dos circunferencias, que pasando por un foco sean tangentes interiores a la focal de centro el otro foco.En la animación inferior puedes ver cómo se aplican dichas nociones en la resolución de este problema.
HIPÉRBOLA.
Aplicando potencia determinamos los centros de dos circunferencias, que pasando por un foco sean tangentes (interior y exterior) a la focal de centro el otro foco.En la siguiente animación te mostramos cómo se definen dichos centros.
PARÁBOLA.
Empleando los conceptos y procedimientos de tangencia y potencia determinamos los centros de las circunferencias que pasando por el foco son tangentes a la recta directriz.En la animación inferior te mostramos la resolución de este ejercicio, puedes comparar su similitud con otros problemas resueltos en el tema de potencia de la unidad didáctica primera.
Pregunta de Elección Múltiple
Solución
Caso de estudio
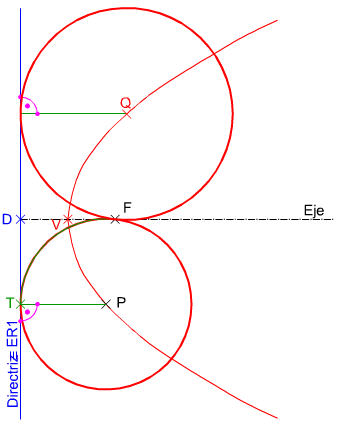 |
En la figura de la izquierda puedes ver cómo se ha determinado el punto Q intersección de una Parábola con una recta alineada con un punto de la curva y su foco. Para resolverlo debes repasar las nociones aprendidas sobre la Parábola en el tema anterior, y aplicar los conceptos y procedimientos explicados en este apartado. Material necesario:
|
| Para realizar este ejercicio debes descargar este documento pdf. |