Parábola

1- ¿Por qué es importante estudiar la parábola?

La parábola es una curva muy común y útil en la vida diaria, y su uso se extiende a muchas áreas de la ciencia y la tecnología. Algunos ejemplos de cómo se utiliza la parábola son:

1. Antenas parabólicas: Las antenas parabólicas se utilizan para transmitir y recibir señales de radio y televisión. La forma de parábola de la antena permite concentrar la señal en un punto focal, lo que permite una mejor recepción y transmisión de la señal.
2. Faros de automóviles: Los faros de automóviles modernos suelen tener una forma parabólica. La curva de la parábola permite que la luz de los faros se concentre en un punto focal, lo que permite una mejor visibilidad en la carretera.
3. Espejos parabólicos: Los espejos parabólicos se utilizan en la energía solar para concentrar la luz del sol en un punto focal, lo que aumenta la cantidad de energía que se puede obtener de los paneles solares.
4. Telescopios: Los telescopios suelen utilizar espejos parabólicos en lugar de lentes para enfocar la luz. La curva de la parábola permite que la luz se refleje en el espejo y se concentre en un punto focal, lo que permite una mejor resolución de la imagen.
5. Arquitectura: La forma de la parábola también se utiliza en la arquitectura. Por ejemplo, la forma de la parábola se puede utilizar en la construcción de puentes y techos para crear estructuras fuertes y estables que soporten grandes cargas.

Estos son solo algunos ejemplos del uso de la parábola. La curva también se utiliza en muchas otras áreas, como la óptica, la acústica y la ingeniería.

2- Qué es una parábola

La parábola es una curva plana que se define como el lugar geométrico de los puntos que están equidistantes de un punto fijo llamado «foco» y una recta fija llamada «directriz». A continuación, te muestro las principales características de la parábola:

1. Foco: Es el punto fijo dentro de la parábola y se ubica en el eje de simetría. Cualquier rayo de luz que provenga del foco y sea reflejado por la parábola se reflejará en una dirección paralela al eje.
2. Directriz: Es una recta fija ubicada fuera de la parábola y perpendicular al eje de simetría. Cualquier punto de la parábola está a la misma distancia del foco que de la directriz.
3. Eje de simetría: Es la recta que divide a la parábola en dos partes iguales y que pasa por el foco.
4. Vértice: Es el punto de la parábola donde se encuentra el eje de simetría y donde la curva cambia de dirección.
5. Longitud focal: Es la distancia entre el foco y el vértice de la parábola.
6. Ecuación: La ecuación de la parábola en su forma estándar es: y = ax^2 + bx + c, donde a, b y c son constantes. La ecuación puede variar dependiendo de la posición y orientación de la parábola.
7. Formas de la parábola: La parábola puede tener diferentes formas, dependiendo de la posición del foco y la directriz. Por ejemplo, si la directriz está en la parte superior de la parábola, ésta tendrá una forma abierta hacia abajo, mientras que si la directriz está en la parte inferior, la parábola tendrá una forma abierta hacia arriba.

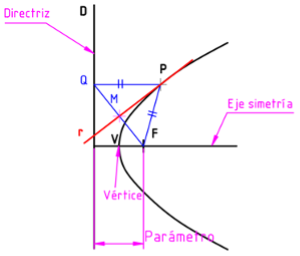
Estos son sus elementos:

• Focos F: al contrario de las otras dos curvas cónicas vistas hasta ahora, la parábola solo tiene un foco fijo. Su distancia a un punto de la curva es el radio vector y su distancia a la directriz es el parámetro. Es el punto de tangencia del plano secante con la esfera inscrita.
• Directrices: es la polar del foco respecto a la parábola, perpendicular a la recta que une el vértice con el foco.
• Excentricidad: la constante de las distancias de un punto de la curva al foco y a la directriz en este caso es 1, dado que la distancia de un punto de la curva al foco es la misma que desde ese punto a la directriz (ortogonalmente).
• Parámetros:
  • Eje perpendicular a la directriz conteniendo al foco F y al vértice V.
  • Vértice V, punto de la curva contenido en el eje, equidistante de la directriz y del foco.
  • Parámetro p como distancia del foco a la directriz.
  • Parámetro 2p como cuerda perpendicular al eje por F.
• Circunferencia principal: es de radio infinito, tangente a la curva en el vértice. Es el lugar geométrico de los pies de las perpendiculares trazadas desde los focos a cada una de las tangentes a la cónica.
• Circunferencia focal: su radio es infinito, coincidiendo con la recta directriz, por ello, los puntos simétricos del foco respecto a cualquier tangente se encuentran en la directriz. Por tanto, es lugar geométrico de los simétricos de los focos respecto de las tangentes a la parábola.

Si atiendes a esta explicación, podrás realizar a partir de aquí todos los ejercicios posibles con la parábola. En consecuencia, te sugiero que imprimas la parábola que te dejo más abajo y dibujes conmigo. Te aseguro que si lo haces, podrás realizar cualquier problema de parábolas que se te ponga por delante:

Imprime esta lámina y dibuja conmigo a la vez que ves el video:

3- ¿Qué son los focos de la parábola y de donde surgen?

Aquí tienes el teorema de Dandelin (que ya viste en la explicación general de las curvas cónicas) aplicado a la parábola. Observando este dibujo, podrás entender de donde salen los diferentes elementos que componen la elipse: focos, directrices y ejes.

¿Preparado para realizar ejercicios sobre la parábola? Aquí puedes descargártelos:

Te dejo algunas soluciones en video:

Te dejo aquí otro ejercicio por si sigues motivado estudiando las parábolas:

Aquí tienes las soluciones en PDF:

Sigue estudiando el resto de curvas cónicas: