2.2. Traslación
Actividad
Mediante la traslación puedes crear formas más complejas: repitiendo una figura básica siguiendo un patrón de filas y columnas.
DEFINICIÓN: La traslación es una transformación Isométrica.
Trasladar una figura plana es aplicar a la misma un movimiento rectilíneo según una dirección dada.
Una figura transformada mediante traslación es igual al original, por tanto, sus lados son paralelos entre sí y los ángulos son iguales.
Trasladar una figura plana es aplicar a la misma un movimiento rectilíneo según una dirección dada.
Una figura transformada mediante traslación es igual al original, por tanto, sus lados son paralelos entre sí y los ángulos son iguales.
ELEMENTOS:
- Elementos característicos: El vector guía (vector de traslación) señala la dirección, el sentido y la magnitud del desplazamiento (AA’, BB’,...).
- Elementos dobles: Las rectas que unen dos puntos.
PROPIEDADES:
Actividad
Cuando se realiza una traslación de un punto A, según vector dado v, se
transforma en otro punto A’ tal que el vector que los une AA’ = v.
APLICACIONES:
- Dadas dos rectas que se cortan r y s, situar un cuadrado, de lado dado, de manera que uno de sus lados coincida en la recta r, y un vértice del lado opuesto pertenezca a la otra recta s:
- Construcción de un mosaico, cuyo módulo es una forma poligonal regular.
Caso de estudio
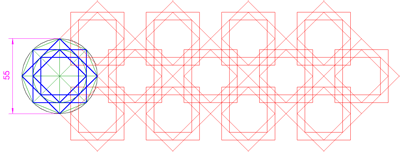Aplicando traslación realiza el mosaico de la imagen izquierda.
¿Necesitas ayuda para resolver este ejercicio?