2.1. Representación
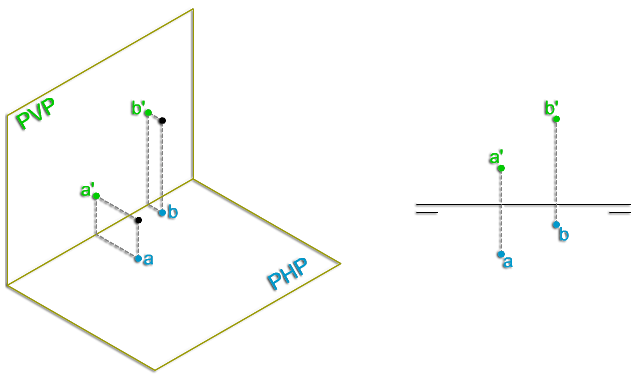
La representación de un punto en el sistema diédrico viene dada por la de sus dos proyecciones, alzado y planta (proyección vertical y horizontal, respectivamente).
Estas dos proyecciones no tienen una posición arbitraria, sino que las líneas de correspondencia que unen la proyección vertical con la horizontal, tiene la misma dirección, es decir, están en correspondencia, alineadas perpendicularmente con la línea de tierra.
De acuerdo con lo explicado en el apartado anterior, coordenadas, las proyecciones del punto se obtienen a partir de tres magnitudes cartesianas: x, y, z, que denominamos: origen, alejamiento y cota, respectivamente.
Importante
El alejamiento y la cota son medidas fijas (no cambian mientras el sistema permanezca inmutable), pero la distancia respecto al origen es relativa, dependiendo de dónde se sitúe ese origen arbitrario.
Al abatir el plano horizontal (PHP) sobre el vertical (PVP), las dos proyecciones del punto quedan unidas por un segmento, llamado línea de referencia, perpendicular a la línea de tierra (LT).
Para poder representar varios puntos en un mismo sistema, a partir de sus coordenadas (origen, alejamiento y cota), tenemos que fijar un punto arbitrario (O), como origen común de todos ellos.
Representar un punto dadas sus coordenadas
En la siguiente animación puedes ver cómo se representa un punto A, dadas sus coordenadas X, Y, Z (origen, alejamiento, cota): 40, 30, 20.
Caso práctico
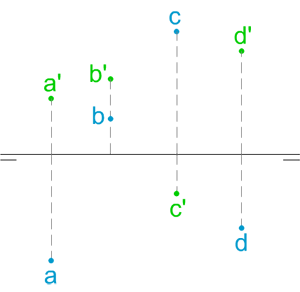De los puntos representados en la imagen izquierda, ¿cuál está más cerca del plano horizontal de proyección (PHP)?. ¿Y del vertical de proyección (PVP)?