1.1. Fundamentos
Nota:
Los elementos de la afinidad son los mismos que los de la homología, exceptuando el centro, que no tiene al ser los rayos o rectas proyectantes paralelas entre sí.
La dirección de afinidad es el ángulo formado por los rayos proyectantes con el eje.
DT2 U2 T4 Apdo. 1.1: fundamentos de la afinidad
Video de Departamento de DIBUJO IEDA alojado en Youtube
Nota:
La característica principal de una afinidad es la relación de distancias a la recta de puntos dobles de los pares de puntos afines (k), siendo este su parámetro o razón de afinidad.
CARACTERÍSTICAS.
- Valor de la constante K. Dependiendo de su valor (negativo o positivo) las figuras afines estarán situadas en cada uno de los semiplanos determinados por el eje de afinidad o en el mismo. En la siguiente animación puedes ver de manera detallada cómo queda representada una figura afín según sea el sentido del parámetro k.
DT2 U2 T4 Apdo. 1.1: valor de la constante k de afinidad
Video de Departamento de DIBUJO IEDA alojado en Youtube
- Posición del vector dirección respecto del eje de afinidad. La posición de las figuras afines también dependerá de cómo esté dispuesto el vector de dirección respecto del eje de afinidad. En la animación inferior te mostramos de forma detallada cómo queda representada una figura afín según un vector oblicuo y otro paralelo. Para determinar los vértices aplicaremos un parámetro k dado.
DT2 U2 T4 Apdo. 1.1: posición del vector de dirección del eje de afinidad
Video de Departamento de DIBUJO IEDA alojado en Youtube
Objetivos
Ortoafinidad.
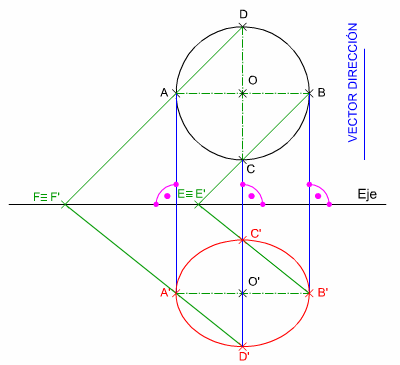Cuando el ángulo el vector dirección forma un ángulo recto (90º) con el eje de afinidad esta se denomina ortoafinidad.
En la figura de la izquierda puedes ver la transformación de una circunferencia mediante ortoafinidad, observa cómo un eje de la curva cónica es paralelo al eje de afinidad.
La ortoafinidad es un recurso muy empelado en los sistemas de proyección (perspectiva caballera y diédrico) pues permite resolver de manera sencilla trazados complejos.
Este tipo de transformaciones se tratarán en otros apartados de este tema.