2.3. Circunferencia
Actividad
Para poder dibujar la figura homóloga de una circunferencia es necesario que dicha homología quede determinada por una de sus rectas límites.
Transformación de una circunferencia en una Elipse.
En la animación inferior puedes ver cómo se ha transformado una circunferencia en una elipse. La rectas tangentes nos determinan diámetros conjugados de dicha curva cónica, por tanto, debemos aplicar los conceptos y procedimientos estudiados en el tema 1 de esta Unidad Didáctica, para poder determinar sus ejes.
Objetivos
La transformación homológica de una circunferencia dependerá de su situación respecto de la recta límite:
- Circunferencia exterior a la recta límite: su transformada es una Elipse.
- Circunferencia secante a la recta límite: su transformada es una Hipérbola, siendo los puntos intersección puntos de las asíntotas.
- Circunferencia tangente a la recta límite: su transformada es una Parábola, el eje de dicha cónica será paralelo a la dirección del segmento formado por el centro de homología y el punto de tangencia.
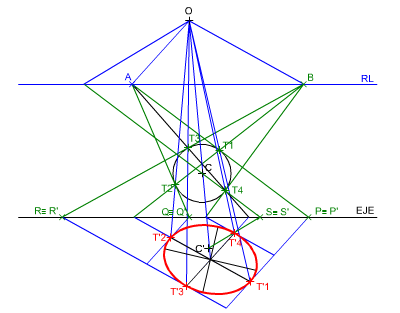 |
En la figura de la izquierda tienes una homología determinada por el centro O, el eje y un par de puntos homólogos (C-C'). Te pedimos que dibujes la transformada de la circunferencia dada. Para resolverlo debes repasar el método explicado en la animación anterior. Material necesario:
|
| Para realizar este ejercicio debes descargar este documento pdf. |