4.1. Elementos fundamentales y simbología

El matemático griego Euclides (ca. 325 a. C.-ca. 265 a. C.) en su obra Los elementos basa su argumentación sobre la geometría plana en un conjunto de axiomas llamados postulados, para el tema que nos ocupa destacaremos los siguientes:
- Por dos puntos se puede trazar una recta que los una.
- Cualquier segmento puede ser prolongado de forma continua en una recta ilimitada.
- Se puede trazar una circunferencia con cualquier centro y cualquier radio dados.
- Todos los ángulos rectos son iguales
En la imagen superior, detalle del fresco la escuela de Atenas de Rafael de Sanzio, puedes ver una representación de Euclides explicando a sus alumnos sus enunciados.
| ELEMENTO | DEFINICIÓN | REPRESENTACIÓN | |
| Punto | No tiene dimensiones, queda determinado por dos rectas que se cortan |
Una cruz pequeña, un círculo y su centro, etc.. Va acompañado de una letra mayúscula. |
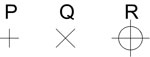 |
| Línea |
Sucesión infinita de puntos. Dependiendo de la dirección que tome esta tendremos:
|
Por dos puntos por los que pasa acompañados de una letra minúscula. | |
| Semirrecta | Recta dividida por un punto llamado origen. | Por el punto origen y otro punto cualquiera por el que pasa. | |
| Segmento | Parte de una recta limitada por dos puntos, llamados extremos. Tiene dimensión | Por sus puntos extremos. | |
| Plano |
Superficie generada por una recta en movimiento. Un plano queda dividido en dos partes llamadas semiplanos. |
Una letra griega o una letra mayúscula. | 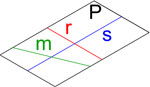 |
Para saber más
Si quieres conocer la vida de Euclides y su principal obra "los elementos" visita este enlace: euclide.org