Resumen
Aquí tienes un resumen de los principales conceptos estudiados en el tema. Nos centraremos en concreto en los triángulos y cuadriláteros: su clasificación, propiedades y métodos de construcción.

Un polígono es una figura plana delimitada por una secuencia de segmentos consecutivos no alineados. Dichos segmentos se denominan lados.
Elementos de un polígono
- Lado: son los segmentos que forman el polígono. También nombradas como aristas.
- Vértice: es el punto de corte entre dos lados.
- Diagonal: es el segmento que une dos lados no consecutivos.
- Perímetro: es el contorno de la superficie del polígono, la suma de las longitudes de todos sus lados
En polígonos regulares también distinguimos los siguientes elementos:
- Centro: Es un punto equidistante de todos los ángulos y lados.
- Apotema: Es el segmento que une el centro del polígono con el punto medio de cualquiera de sus lados.
- Radio: Es el segmento que une el centro del polígono con cualquiera de sus vértices.
- Ángulo central: es el formado por dos radios que parten del centro a los dos extremos de un mismo lado.
Clasificación de polígonos
Según su forma:
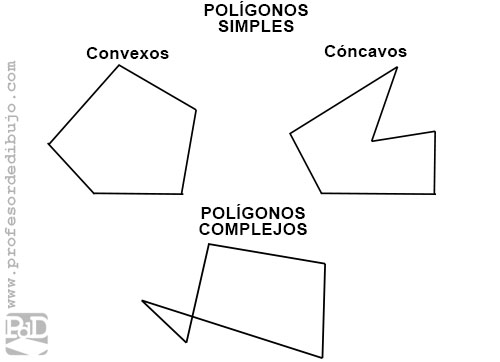
- Simple: Cuando ninguno de sus lados no consecutivos se cortan.
- Convexo: es aquel polígono que tiene todos sus ángulos interiores menores que 180º. Se cumple que al ser atravesado por una recta siempre lo corta en un máximo de dos puntos.
- Cóncavo: es aquel polígono que tiene alguno o varios de sus ángulos interiores menores que 180º. Se cumple que al ser atravesado por una recta puede cortarlo en más de dos puntos.
- Complejo: Cuando dos de sus aristas no consecutivas se cortan.
Según sus condiciones de regularidad:
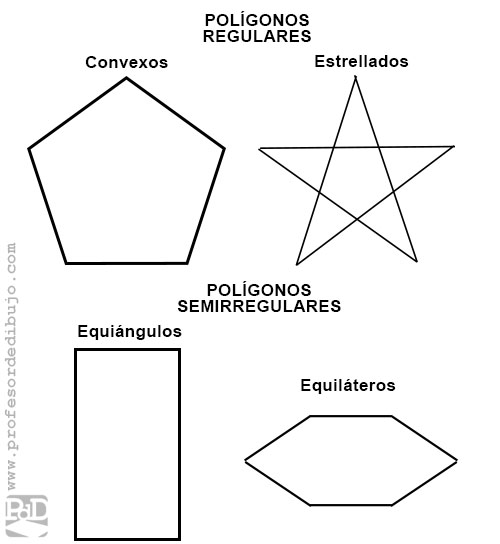
- Regular: son polígonos que tienen todos sus lados y ángulos iguales. Dentro de los regulares encontramos dos tipos:
- Convexos: Son polígonos simples convexos cuyos lados y ángulos son todos iguales.
- Estrellados: Son polígonos regulares cóncavos cruzados con forma de estrella.
- Semirregulares: Son aquellos que tienen todos sus lados o todos sus ángulos iguales, pero no ambos elementos. Distinguimos dos tipos:
- Equiángulo: Son polígonos que tienen todos sus ángulos iguales, pero no sus lados.
- Equilátero: Son polígonos que tienen todos sus lados iguales, pero no sus ángulos.
- Irregular: son aquellos polígonos que tienen lados y ángulos diferentes.
Relaciones del polígono respecto a la circunferencia
Se contemplan dos tipos de relaciones:
- Inscrito: Se dice que un polígono esta inscrito en una circunferencia cuando todos los vértices del polígono son puntos de dicha circunferencia.
- Circunscrito: Se dice que un polígono está circunscrito a una circunferencia cuando todos los lados del polígono son tangentes a dicha circunferencia.

Polígonos según el número de lados
| Nombre | Nº de lados |
| TRIÁNGULO | 3 LADOS |
| CUADRILÁTEROS | 4 LADOS |
| PENTÁGONO | 5 LADOS |
| HEXÁGONO | 6 LADOS |
| HEPTÁGONO | 7 LADOS |
| OCTÓGONO u OCTÁGONO | 8 LADOS |
| ENEÁGONO u NONÁGONO | 9 LADOS |
| DECÁGONO | 10 LADOS |
| ENDECÁGONO | 11 LADOS |
| DODECÁGONO | 12 LADOS |
Nominación
Los vértices y lados se nombrarán con letras a partir de la «a» y en sentido contrario al de las agujas del reloj. Los ángulos con letras en mayúscula y los lados con la letra del vértice opuesto, pero en minúscula.
Importante
- Una figura plana puede quedar delimitada por la intersección o unión de líneas rectas, curvas o la combinación de ambas. Si se emplean solamente líneas rectas la figura plana se denomina polígono.
- Dependiendo del número de lados los polígonos pueden ser: triángulos, cuadriláteros, pentágonos, hexágonos, etc.
- Dependiendo de cómo sean sus lados podemos clasificarlos en regulares ( si todos sus lados y ángulos son iguales) e irregulares ( si no todos sus lados y ángulos son iguales) .
- El término polígono proviene del griego poli (varios) y gono (ángulo). Figuras planas y cerradas delimitadas por rectas que se cortan dos a dos. El polígono es la superficie y la línea poligonal es el perímetro.
- Generalmente para determinar el número de datos necesarios para la construcción de un polígono cualquiera, se aplica la siguiente fórmula: 2n -3 , donde n es el número de lados o vértices. Pero dependiendo del tipo de polígono y sus propiedades o características que de él conozcas este número de datos necesarios disminuye.
Importante
- En todo polígono podemos encontrar los siguientes elementos: a)Lineales: lado, vértice, diagonal, altura, perímetro, radio y apotema, este último se da en los polígonos regulares b)Elementos angulares: ángulo interior, exterior y central, este último se da en los polígonos regulares.
- El método que debes seguir en la construcción de un polígono depende de sus elementos, características y propiedades que de él conozcas y los procedimientos que debas realizar.
- Directo: lados, diagonales, ángulos o alturas. Para dibujar el polígono sólo necesitas transportar los datos y realizar un procedimiento sencillo.
- Lugares geométricos: mediatrices, bisectrices,arco capaz, etc. Para trazar el polígono debes deducir algunos datos y realizar varios procedimientos más complejos.
- Transformación geométrica: traslación, simetría, giro, homotecia. (Estos procedimientos no se aplican en este tema).
Importante
Clasificación y propiedades
- Dependiendo de la posición de sus lados los polígonos se clasifican en convexos, cóncavos y estrellados
- A su vez los polígonos convexos se clasifican en : irregulares, regulares, equiángulos, equiláteros.
- Los polígonos convexos tienen una amplia gama de propiedades( estudiaremos 4 en concreto) que los hacen especialmente útiles en la resolución de problemas de geometría.
-
Todos los polígonos regulares tienen una circunferencia circunscrita e inscrita; el resto de polígonos convexos para que tengan una u otra circunferencia ha de cumplir una serie de condiciones que estudiaremos más adelante.
- Todos los triángulos son polígonos convexos. Todos los polígonos regulares son convexos, salvo los polígonos estrelladosregulares.
Esquema de la clasificación de triángulos

Esquema de la clasificación de cuadriláteros
