1.2. Con cuadriláteros
Nota:
Debes de repasar las fórmulas para calcular la superficie de los principales polígonos (apartado 1. Generalidades) y relacionarlas entre sí.
Triángulo equivalente a un paralelogramo rectángulo.
Se trata de dibujar un triángulo equivalente a un paralelogramo rectángulo cuya base sea igual al lado mayor de dicho cuadrilátero. Relacionamos las fórmulas de ambos polígonos
Triángulo = (base * altura) / 2 = Paralelogramo rectángulo = lado mayor * lado menor.
Por tanto, la altura del triángulo debe de ser igual al doble del lado menor del paralelogramo rectángulo.
En la animación inferior puedes ver cómo se ha dibujado un triángulo equivalente a un paralelogramo rectángulo de igual base.
DT2 U1 T2 Apdo. 2.2: triángulo equivalente a un paralelogramo rectángulo
Video del Departamento de DIBUJO IEDA alojado en Youtube
Triángulo equivalente a un cuadrado.
En este ejercicio se quiere trazar un triángulo equivalente a un cuadrado dado, de altura mayor al lado de dicho cuadrilátero. Para dibujarlo podemos aplicar el método general estudiado en el apartado anterior y después transformar el triángulo obtenido en otro de distinta base y altura.
Si queremos simplificar el trazado podemos recurrir a un método particular que nos permite dibujar dicho triángulo equivalente de forma directa. Este procedimiento está basado en la proporcionalidad de segmentos:
Como el lado BC del cuadrado es media proporcional de los segmentos EB y BF, podemos deducir:
- Superficie del cuadrado = BC2 = EB * BF
- Superficie del triángulo = (EB * BG) /2. Si sustituimos BG = 2BF = (EB * 2BF) = EB * BF.
Por tanto, Superficie del cuadrado = Superficie del triángulo.
DT2 U1 T2 Apdo. 2.2: Triángulo equivalente a un cuadrado
Video del Departamento de DIBUJO IEDA alojado en Youtube
Objetivos
Triángulo equivalente a un rombo.
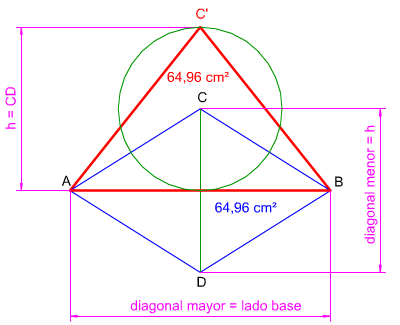
Dibujar un triángulo equivalente a un rombo, de base igual a una de sus diagonales, es muy sencillo. Solamente debemos relacionar sus fórmulas:
- Superficie del triángulo = (base * altura) /2.
- Superficie del rombo = (diagonal mayor * diagonal menor) /2
Por lo que podemos deducir que la altura del triangulo debe de tener una longitud igual a la de la otra diagonal.
En la imagen de la izquierda puedes ver cómo se dibujado un triángulo isósceles equivalente a un rombo dado, de lado base AB igual a la diagonal mayor AB de dicho paralelogramo. La altura del triángulo lógicamente debe de tener una longitud igual a la diagonal menor del rombo.
Caso de estudio
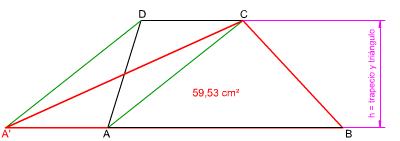 |
En la figura de la izquierda puedes ver cómo se ha trazado un triángulo A'BC equivalente a un trapecio dado ABCD, siendo su altura la misma que la de dicho cuadrilátero. Para resolverlo debes de aplicar el método general explicado en el apartado 1. Material necesario:
|
| Para realizar este ejercicio debes descargar este documento pdf. |