2.2. Cuadrado
Importante
Para poder dibujar un cuadrado equivalente a cualquier polígono, normalmente primero debemos transformarlo en un paralelogramo rectángulo equivalente.
Existen métodos particulares que nos permiten trazar cuadrado equivalente de manera directa.
Sea cual sea el método elegido, debemos aplicar los conceptos y procedimientos empelados en el dibujo de un segmento media proporcional.
Cuadrado equivalente a un rectángulo.
La resolución de este ejercicio está basada en los conceptos y procedimientos empleados en el apartado anterior "rectángulo equivalente a un cuadrado".
En este caso el trazado es más sencillo, ya que solamente debemos determinar la media proporcional de los lados mayor y menor del paralelogramo rectángulo dado.
En la animación inferior se ha determinado el cuadrado A'B'C'D' equivalente al paralelogramo rectángulo ABCD dado mediante el teorema del cateto.
DT2 U1 T2 Apdo. 3.2: cuadrado equivalente a un rectángulo
Video del Departamento de DIBUJO IEDA alojado en Youtube
Objetivos
Cuadrado equivalente a otros dos dados.
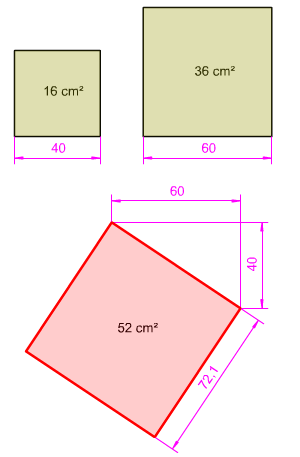
Para calcular el lado de un cuadrado equivalente a la suma de otros dos dados debemos aplicar el teorema de Pitágoras: a2 + b2 = c2
El lado solución será la hipotenusa de un triángulo rectángulo, siendo los catetos los lados de los cuadrados dados, el procedimeinto sería el siguiente:
- Se disponen dos segmentos ortogonalmente siendo sus magnitudes igual al lado de cada uno de los cuadrados dado (40 y 60).
- Se completa el triángulo rectángulo, cuyos catetos serán los lados anteriores y la hipotenusa el lado del cuadrado buscado.
- Se construye el cuadrado disponiendo dos de los lados perpendicularmente y otro paralelo respecto de la hipotenusa anterior.
En la imagen izquierda puedes ver cómo se ha resuelto este ejercicio.
Cuadrado equivalente a un rombo.
En este caso primero debemos transformar el rombo ABCD dado en un paralelogramo rectángulo ACPQ equivalente, para finalmente dibujar un cuadrado A'B'CD' equivalente a dicho paralelogramo.
En la siguiente animación pues ver cómo primero dibujamos un paralelogramo rectángulo equivalente al rombo dado y después, aplicando el teorema de la altura, trazamos el cuadrado equivalente.
DT2 U1 T2 Apdo. 3.2: cuadrado equivalente a un rombo
Video del Departamento de DIBUJO IEDA alojado en Youtube
Cuadrado equivalente a un polígono regular.
Este método particular nos permite dibujar, de manera directa, un cuadrado equivalente a cualquier polígono regular, por lo que no es necesario convertir previamente dicho polígono en un paralelogramo rectángulo.
Como la superficie de cualquier polígono regular se calcula multiplicando su apotema por el semiperímetro, la media proporcional de ambos segmentos será el lado del cuadrado equivalente.
En la animación inferior se ha dibujado un cuadrado equivalente a un hexágono regular dado mediante el teorema de la altura.
DT2 U1 T2 Apdo. 3.2: cuadrado equivalente a un hexágono
Video del Departamento de DIBUJO IEDA alojado en Youtube
Pre-conocimiento
La cuadratura del círculo: cuadrado equivalente a un círculo.
-
La cuadratura del círculo es un problema matemático, y geométrico, irresoluble en el que se pretende, mediante el uso del compás y la regla, dibujar un cuadrado de área equivalente a un círculo dado.
- Cuadrado = l2
- Círculo:
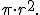
Relacionamos las fórmulas del cuadrado y del círculo:
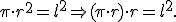
-
Si queremos trazar un cuadrado equivalente a un círculo, de manera aproximada, primero tenemos que dibujar un paralelogramo rectángulo equivalente, siendo la longitud de su lado mayor igual a la mitad de la rectificación de la circunferencia del círculo, y su lado menor al radio. Finalmente mediante el teorema de la altura determinamos el lado del cuadrado.
- Obtenemos la rectificación de la semicircunferencia determinando el segmento MN.
- Al anterior segmento (MN) le sumamos la longitud del radio de la circunferencia obteniendo el punto P.
- Calculamos la media proporcional de los segmentos PM y MN, obteniendo el segmento MRP.
- El segmento anterior (MR) es el lado del cuadrado buscado.
Caso de estudio
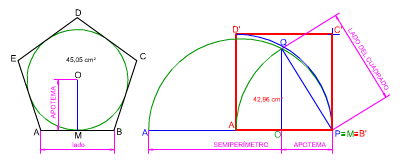 |
En la imagen izquierda tienes el dibujo de un cuadrado A'B'C'D' equivalente a un pentágono regular dado ABCDE Para resolver este ejercicio hemos aplicado el teorema de la altura, determinando así el lado del cuadrado que será media proporcional de la apotema del polígono y su semiperímetro. Material necesario:
|
| Para realizar este ejercicio debes descargar este documento pdf. |