2.1. Rectángulos
Rectángulo equivalente a un triángulo.
Para elaborar este ejercicio debemos de proceder de manera inversa a lo realizado en el apartado 2.2. "triángulo equivalente a un paralelogramo rectángulo"
En la animación inferior puedes ver su desarrollo.
DT2 U1 T2 Apdo 3.1: rectángulo equivalente a triángulo manteniendo la base
Video del Departamento de DIBUJO IEDA alojado en Youtube
Rectángulo equivalente a otro dado.
Para resolver este ejercicio tenemos que aplicar los conceptos y procedimientos desarrollados en la resolución del "triángulo equivalente a otro dado de distinta base" del apartado 2.2, ya que el paralelogramo rectángulo dado está compuesto por dos triángulos rectángulos.
En la siguiente animación puedes ver cómo el lado mayor AB del paralelogramo ABCD dado, se corresponde con el cateto mayor del triángulo rectángulo ABD, su lado menor AD con la altura de dicho triángulo, siendo la diagonal BD la hipotenusa. El lado A'B' del otro paralelogramo rectángulo equivalente A'B'C'D' será el cateto mayor del triángulo rectángulo A'B'D' equivalente al ABD.
DT2 U1 T2 Apdo. 3.1: rectángulo equivalente a otro dado
Video del Departamento de DIBUJO IEDA alojado en Youtube
Objetivos
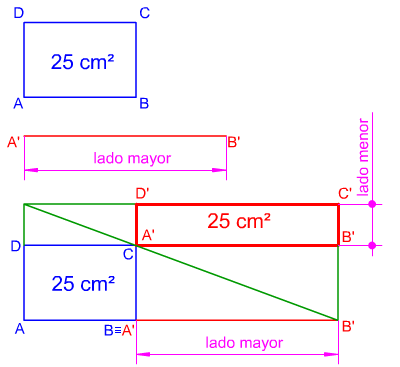
Para dibujar un paralelogramo rectángulo equivalente a otro dado podemos
emplear un método basado en la proporcionalidad de segmentos
En la imagen de la izquierda se ha trazado un paralelogramo
rectángulo A'B'C'D' equivalente al dado ABCD, conocido su lado mayor
A'B'. Observa cómo los segmentos AB y A'B' son proporcionales, como
también lo son los segmentos AD y B'C', cumpliéndose:
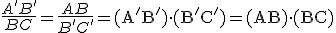
Rectángulo equivalente a un cuadrado.
La equivalencia entre un paralelogramo rectángulo y un cuadrado, y viceversa, está basada en la media proporcional entre los lados del primero.
Recordemos que el segmento media proporcional de dos segmentos dados es la raíz cuadrada del producto de ambos.
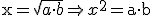
Así pues, todo cuadrado cuyo lado sea media proporcional de los lados mayor y menor de un paralelogramo rectángulo, resultará equivalente a este.
Para poder dibujar un paralelogramo rectángulo equivalente a un cuadrado dado es necesario conocer un lado (normalmente será el menor).
En la animación inferior puedes ver cómo se ha determinado el lado menor aplicando el teorema de la altura.
DT2 U1 T2 Apdo. 3.1: rectángulo equivalente a un cuadrado
Video del Departamento de DIBUJO IEDA alojado en Youtube
Pre-conocimiento
Rectángulo equivalente a un rombo.
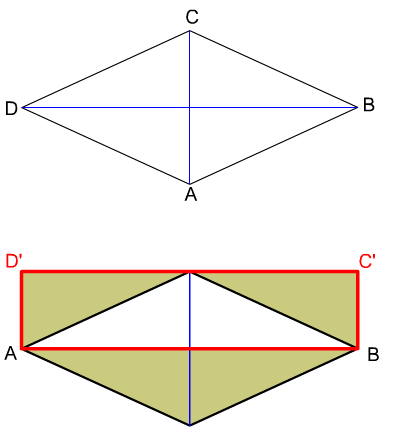
Para dibujar un paralelogramo rectángulo equivalente a un rombo tenemos
que aplicar los conceptos y procedimientos desarrollados en el apartado
2.2 "triángulo equivalente a un rombo".
En este caso concreto la similitud de ambos paralelogramos facilita su trazado:
- Superficie del paralelogramo rectángulo = (lado mayor * lado menor).
- Superficie del rombo = (diagonal mayor * diagonal menor) /2.
Por tanto, como la longitud del lado mayor del paralelogramo rectángulo debe de ser igual a la de la diagonal mayor del rombo, el lado menor del paralelogramo rectángulo equivalente debe de ser igual a la mitad de la diagonal menor del rombo dado.
En la imagen inferior izquierda puedes ver cómo los triángulos rectángulos en que queda divido un rombo, una vez trazadas sus diagonales, son los mimos que componen el paralelogramo rectángulo equivalente.
Caso de estudio
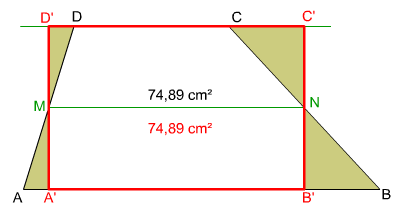
En la imagen izquierda tienes el dibujo de un paralelogramo rectángulo A'B'C'D' equivalente a un trapecio escaleno dado ABCD, siendo su altura la misma que la de dicho cuadrilátero.
Observa cómo los triángulos AA'M y MDD' son equivalentes, como también lo son los triángulos B'BN y NC'C.
Material necesario:
- Lápiz blando y duro.
- Compás.
- Plantilla de dibujo (escuadra y cartabón).
- Hojas para realizar trazados de prueba.
| Para realizar este ejercicio debes descargar este documento pdf. |