2.3. El plano
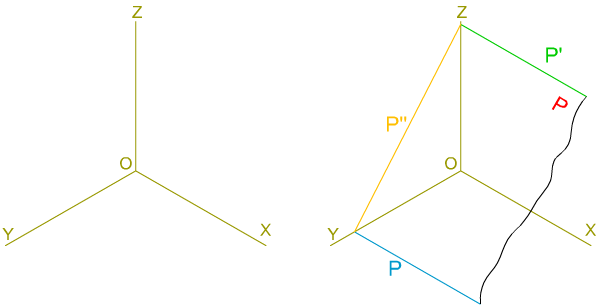
Recordemos que las caras de una forma, objeto, poliedro, etc., son planos delimitados por aristas (rectas) y vértices (puntos).
En la imagen superior tienes la perspectiva isométrica de un plano determinado por las rectas generadas por la intersección de dicho plano con las caras del triedro trirrectángulo.
Actividad
TRAZAS.
En el sistema axonométrico un plano queda definido por sus trazas con las caras del triedro trirrectángulo.
Estas trazas son rectas contenidas en dichas caras del triedro, por tanto, tienen su proyección directa confundida con la secundaria de dicho plano; las otras proyecciones secundarias estarán situadas en los ejes isométricos.
Para simplificar su representación solamente dibujaremos la proyección secundaria que coincide con la directa de cada una de las trazas.
Objetivos
 Todo plano oblicuo tiene, además de las trazas con los planos del triedro trirrectángulo, una cuarta traza con el plano del cuadro, llamada traza ordinaria.
Todo plano oblicuo tiene, además de las trazas con los planos del triedro trirrectángulo, una cuarta traza con el plano del cuadro, llamada traza ordinaria.Su aplicación principal es la del trazado de abatimientos. que estudiaremos en el curso siguiente.
En la imagen izquierda puede ver la traza ordinaria de una de las caras del triedro.
En la unidad anterior estudiamos cómo se determinaba un plano en el sistema diédrico, recordémoslo: por tres puntos no alineados, por un punto y una recta, por dos rectas que se cortan y por dos rectas paralelas.
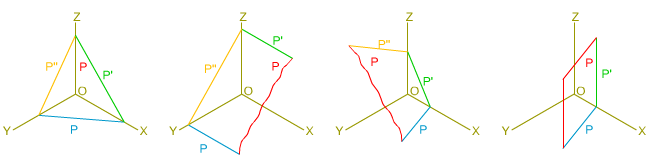
En el sistema axonométrico, y en el isométrico en particular, un plano queda definido de la misma forma. En la imagen inferior tienes dos ejemplos de determinación de un plano, de izquierda a derecha: por tres puntos y por dos rectas que se cortan.
RECTA Y PUNTO CONTENIDOS EN UN PLANO.
Para determinar la pertenencia de un punto y una recta a un plano en el sistema isométrico aplicaremos los conceptos y procedimientos empleados en el sistema diédrico:
- Si una recta pertenece a un plano todos sus puntos deben estar contenidos en el plano. La forma más simple de comprobar si una recta pertenece a un plano, o no, consiste en determinar que las trazas de la recta están contenidas en las respectivas trazas del plano.
- Si un punto pertenece a una recta y esta pertenece a un plano, el punto también está contenido en dicho plano.
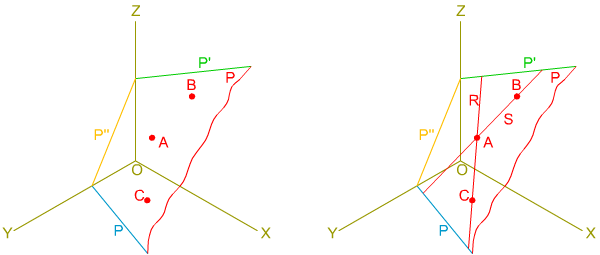
En la imagen inferior te mostramos la pertenencia de una recta y varios puntos a un plano.
Como hemos hecho con el punto y la recta, analizaremos las posiciones de un plano, situado en el primer triedro, respecto de los planos de dicho triedro trirrectángulo, considerando las siguientes posibilidades: paralelos a las caras y los ejes del triedro, y que pasen por dichos ejes.
En la animación inferior puedes ver, con detalle, dichas disposiciones.
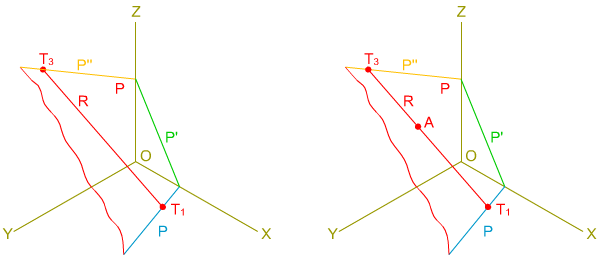
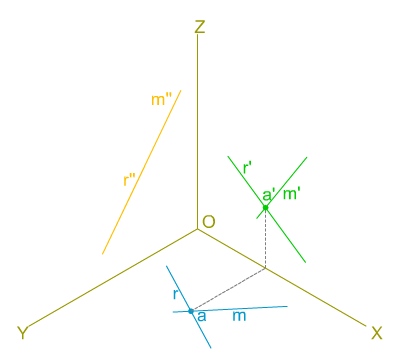 En la imagen izquierda tienes las proyecciones isométricas secundarias
de dos rectas que se cortan (M y R) que pertenecen a un plano P; tienes que determinar las trazas de las rectas y del plano P, y realizar el
dibujo
isométrico de las proyecciones directas de las rectas.
En la imagen izquierda tienes las proyecciones isométricas secundarias
de dos rectas que se cortan (M y R) que pertenecen a un plano P; tienes que determinar las trazas de las rectas y del plano P, y realizar el
dibujo
isométrico de las proyecciones directas de las rectas.