1.1. Elementos
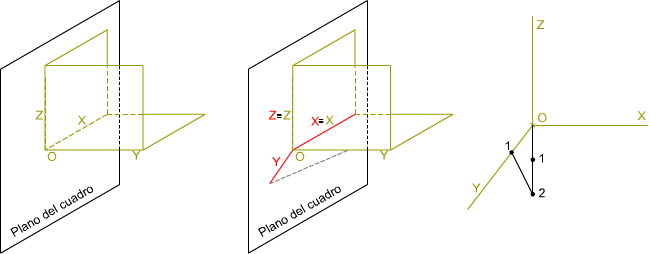
La disposición perpendicular de uno de dos de los planos del triedro respecto del plano del cuadro determina que la proyección sea oblicua, ya que si proyectamos ortogonalmente sobre el plano del cuadro, las proyecciones secundarias estarían confundidas con los ejes X y Z. La dirección de esta proyección oblicua al plano del cuadro puede ser cualquiera, y determina tanto el tipo de perfil como el coeficiente de reducción a aplicar.
En la imagen superior puedes ver cómo se proyectan los ejes isométricos sobre el plano del cuadro y el coeficiente de reducción que se genera.
Los ejes
El ángulo XY depende de dos factores:
- Las características de la forma, figura, pieza, sólido, etc.. que debamos representar.
- El efecto que deseemos darle a la perspectiva:
- Si queremos que las caras de la pieza perpendiculares al plano del cuadro (XOZ) se muestren de igual forma, el ángulo XY debe ser de: 45º, 135º, 225º ó 315º.
- Por el contrario, si necesitamos que alguna de las caras de la pieza laterales se muestren con mayor detalle, el ángulo XY debe ser de: 30º, 60º, 120º, 150º, 210º, 240º, 300º y 330º.
En todo caso, estos ángulos quedan limitados a aquellos que se pueden trazar con la escuadra y el cartabón.
La posición del eje Y depende de la orientación del vector de dirección al proyectarse en el plano del cuadro. En la siguiente animación puedes ver cómo él ángulo formado por los ejes XY delimita el espacio en cuatro cuadrantes, los ángulos se toman en el sentido de las agujas del reloj:
- Ángulo mayor de 0º y menor de 90º: perfil izquierdo, vista superior.
- Ángulo mayor de 90º y menor de 180º: perfil derecho, vista superior.
- Ángulo mayor de 180º y menor de 270º; perfil izquierdo, vista inferior.
- Ángulo mayor de 270º y menor de 360º: perfil derecho, vista inferior.
En la animación inferior puedes ver el efecto que produce sobre una misma figura distintos ángulos XY.
Importante
La posición del eje Y (ángulo XY) dependerá de la posición de los detalles del objeto a representar y de las caras que se quieran visualizar.
Curiosidad
Comparativa entre isométrico, caballera y hejduk
Imagen de Departamento de DIBUJO IEDA en Flickr. Licencia CC
Perspectiva egipcia o de Hejduk
En este tipo de perspectiva el ángulo XY es de 90º y no se aplica coeficiente de reducción. El alzado y la planta se superponen formando una única pieza.
Se puede decir que es una síntesis de la axonometría oblicua frontal y planimétrica.
El principal uso de esta perspectiva es la representación de edificios y de forma más concreta en el dibujo de planos de ciudades.
En las ciudades formadas por calles rectangulares, el empleo de este tipo de perspectiva facilita mucho el trazado.
Coeficiente de reducción
Es la relación entre la proyección de un segmento del eje Y, y su longitud real en el espacio.
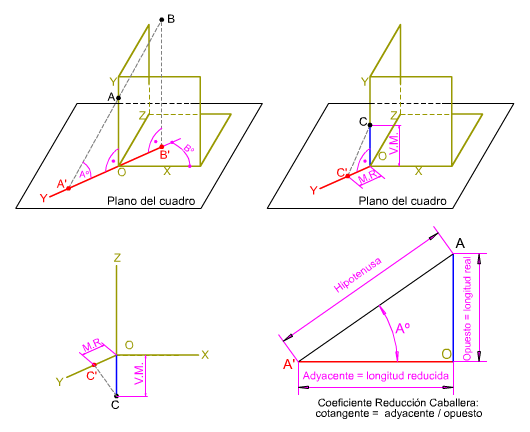
En la imagen superior tienes un aexplicación gráfica del coeficiente de reducción:
La dirección de la proyección oblicua queda definida por los ángulos Aº y Bº.
- Ángulo Aº: es el formado por los rayos proyectantes con el plano del cuadro.
- Ángulo Bº: es el formado por los rayos proyectantes con el plano XOY.
Si proyectamos el punto A según la dirección de proyección oblicua su proyección (A') coincidirá con la proyección del eje Y, formándose el triángulo rectángulo A'OA. La longitud del cateto OA, situado en el espacio, está proyectada en OA', aplicando trigonometría podemos decir que: 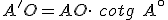
Ejemplo: en un triángulo con lados de 4, 3 y 5, la cotangente del ángulo formado por los lados de longitud 3 y 5 es 3/4
Dependiendo del valor del ángulo Aº la proyección de cualquier magnitud real situada en el eje Y sufrirá una determinada deformación:
- Si el ángulo Aº = 45º su cotangente es igual a la unidad AO = A'O. Toda longitud paralela o contenida en el eje Y se proyecta sin deformación (escala 1:1).
- Si el ángulo Aº es menor de 45º su cotangente es mayor que la unidad. Toda longitud paralela o contenida en el eje Y se proyecta ampliada (escala 2/1, 3/2, .)
- Si el ángulo Aº es mayor de 45º su cotangente es menor que la unidad. Toda longitud paralela o contenida en el eje Y se proyecta reducida (escala 1/2, 2/3, .)
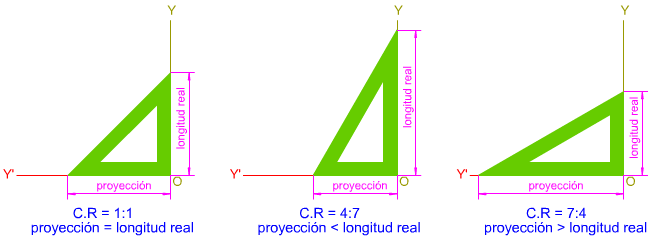
Coeficiente de reducción gráfico. Las magnitudes se pueden reducir multiplicando su valor real por el coeficiente de reducción: (1/2 ó 0,5 por ejemplo), pero esto nos puede dar longitudes con decimales, lo que en dibujo técnico no suele ser operativo.
Para solventar este inconveniente podemos recurrir a la construcción gráfica de dicho coeficiente de reducción, como si de una escala se tratara.
En la animación inferior tienes varios ejemplos de construcción gráfica de los coeficientes de reducción más usuales: 1/2, 2/3 y 3/4.
Para saber más
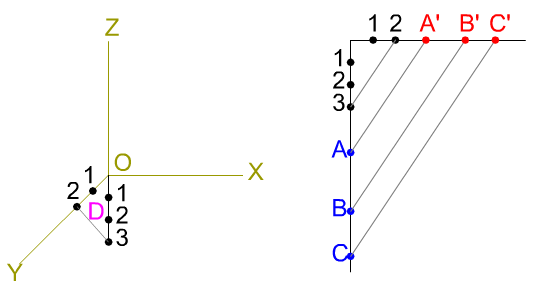
Cuando en una pieza las longitudes paralelas al eje Y son numerosas, el cálculo de la reducción de las mismas complica el trazado.
Para solventar este problema, podemos recurrir a la construcción de un triángulo de reducción, este es un triángulo rectángulo cuyos catetos son proporcionales al coeficiente de reducción.
En la imagen superior tienes un ejemplo de triángulo de reducción para un coeficiente de reducción 2/3. Observa cómo el trazado de las reducciones es más rápido y evita un exceso de trazado en la perspectiva.
Curiosidad
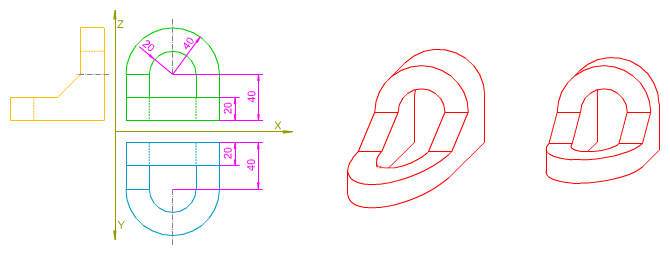
Si no aplicamos coeficiente de reducción obtendremos una perspectiva irreal, en la que las longitudes respecto del eje Y, se mostrarán ampliadas, lo que contraviene todas las leyes de la percepción.
En la imagen superior puedes apreciar la sensación que se obtiene en la perspectiva caballera de una pieza, con coeficiente de reducción y sin él.
