2.2. La recta
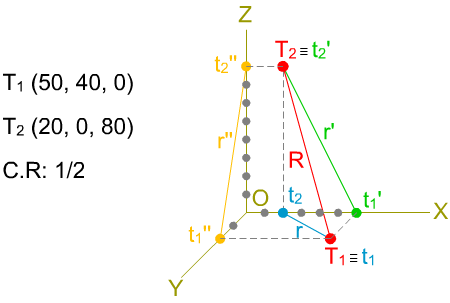
En caballera también necesitamos dos puntos de una recta para poder obtener sus proyecciones, que, como en el caso del punto, serán cuatro: una directa y tres secundarias.
Como hemos hecho con el punto, solamente vamos a analizar a la recta situada en el primer triedro.
Trazas de la recta
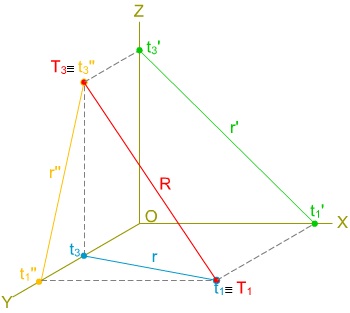
Recordemos que los puntos más notables de una recta quedan definidos por la intersección de esta con las caras del triedro, sus trazas.
Las notaciones de las trazas en caballera son las mismas que hemos empleado en el sistema isométrico.
En la imagen superior se muestra una recta R que corta a los planos del triedro: al plano XOY en T1, y al ZOY en T3. Observa cómo dichas trazas quedan alineadas.
En la animación inferior puedes ver cómo se determinan las trazas de una recta determinada por dos puntos.
Alfabeto de la recta
Vamos a analizar la disposición de una recta respecto de los planos de dicho triedro trirrectángulo, considerando las siguientes posibilidades: contenidas en un plano del triedro, paralelas a los planos del triedro, perpendiculares a un plano del triedro, cortan a un eje del triedro y que pasan por el origen.
En la animación inferior puedes ver, con detalle, dichas disposiciones.
Caso práctico
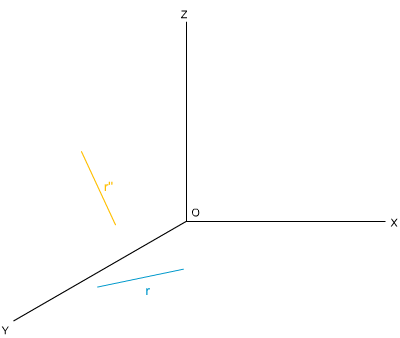
En la imagen superior tienes la perspectiva caballera de las proyecciones secundarias r y r'' de una recta R; tienes que determinar sus trazas y realizar la perspectiva caballera de las proyecciones secundaria r' y directa R.
Para realizar este ejercicio debes descargar este documento pdf.