2.1 Paralelismo: recta y plano
El paralelismo se da entre rectas, entre planos y entre recta y plano.
Es un caso particular de intersección, ya que los elementos geométricos paralelos (rectas y planos) son impropios recíprocamente:
- Las rectas paralelas, entre sí o a un plano, tienen en común un punto impropio.
- Los planos paralelos se cortan en una recta impropia.
Para entender el paralelismo entre estos dos elementos (recta y plano) tenemos que estudiar primero las condiciones que se deben dar para que dos rectas sean paralelas; ya que para que una recta y un plano sean paralelos, la recta tiene que ser paralela a una recta cualquiera contenida en dicho plano.
Considerando lo anterior toda recta horizontal o frontal deberá tener su proyección horizontal o vertical, respectivamente, paralela a la traza homónima del plano al que es paralelo.
Entre rectas
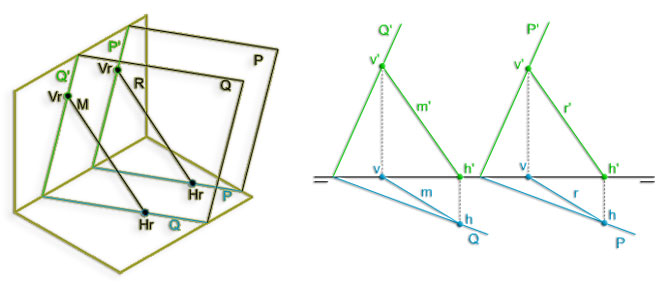
Si dos rectas R y S son paralelas en el espacio, también lo son sus proyecciones diédricas recíprocamente: r' con s' y r con s.
Del mismo modo se puede asegurar que si las proyecciones diédricas (homónimas) de dos rectas son paralelas, las rectas en el espacio también lo son. Excepto las rectas de perfil, pues, aunque sus proyecciones sean paralelas, en el espacio pueden no serlo.
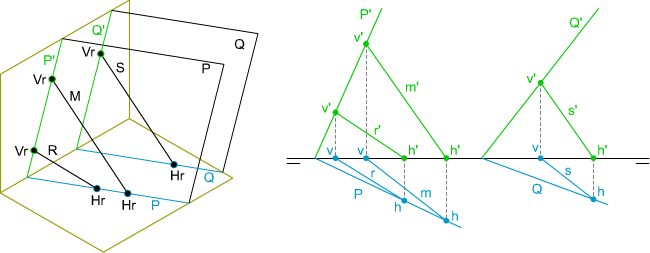
En la imagen inferior puedes ver como rectas que pertenecen a un mismo plano pueden no ser paralelas, pero una de ellas sí lo es respecto de otra que pertenece a un plano no paralelo: las rectas M y R, que pertenecen al plano P no son paralelas entre sí, pero la recta S, que pertenece a un plano Q no paralelo a P, sí es paralela respecto de la recta M.
Para saber más
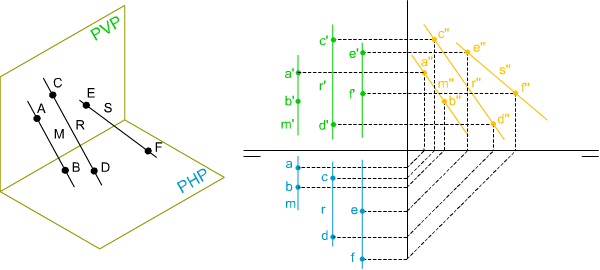
INDETERMINACIÓN DE PARALELISMO ENTRE RECTAS DE PERFIL.
Las rectas de perfil siempre tienen sus proyecciones homónimas paralelas, y aún así puede que no sean paralelas entre sí.
Para poder determinar si dos rectas son paralelas debemos obtener una tercera proyección de cada una de ellas, mediante un plano de perfil, que nos indicará si existe o no paralelismo.
En la imagen superior mediante un perfil (m'', r'' y s''), se puede comprobar que las rectas M y R son paralelas, mientras que la S no lo es.
Entre recta y plano
Para que una recta sea paralela a un plano debe ser, al menos, paralela a una recta cualquiera de dicho plano.
Entre planos
Si dos planos P y Q son paralelos en el espacio, sus trazas también lo son. Al cortar estos planos a otro plano cualquiera (T) genera rectas paralelas.
Excepto los planos paralelos a la LT, pues aunque sus trazas son paralelas, en el espacio pueden cortarse.
DT1 U3 T4 Apdo. 2.1: Plano paralelo a otro plano
Vídeo de Departamento DIBUJO IEDA alojado en Youtube
Caso práctico
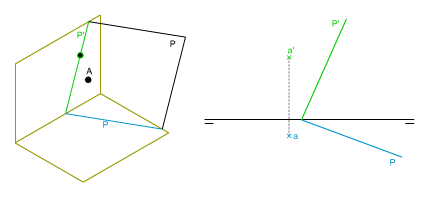
En la imagen superior tienes las proyecciones diédricas y la perspectiva isométrica de las trazas del plano P, y del punto A exterior a dicho plano, tienes que dibujar otro plano Q paralelo a P y que pase por A.
Para realizar este ejercicio debes descargar este documento pdf.