3.2. Recta
Distancia de un punto a una recta
La distancia entre un punto y una recta, situados en el espacio, es el segmento determinado por dicho punto y la intersección de la recta con un perpendicular a ella trazada desde el punto.
Para poder determinar este segmento distancia tenemos que contener el punto en un plano perpendicular a la recta, y seguir el procedimiento que se explica en la siguiente animación:
Distancia entre rectas paralelas
La distancia entre dos rectas paralelas quedará definida por el segmento determinado mediante la intersección de ambas rectas por un plano perpendicular a ellas.
Para calcular la longitud de este segmento tenemos que trazar un plano perpendicular a las dos rectas paralelas y determinar los puntos intersección de ambas en dicho plano, según se explica en la siguiente animación:
Para saber más
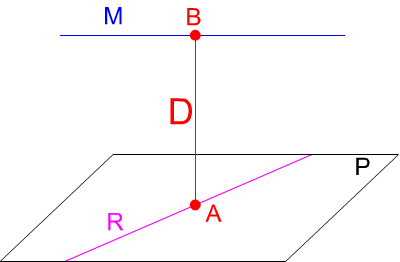
La distancia entre dos rectas que se cruzan es variable, determinar la mínima distancia entre ambas rectas puede resultar complejo cuando ninguna de ellas es perpendicular a uno de los planos de proyección (recta vertical o de punta); en este caso podemos simplificar el método a seguir conteniendo una de las rectas en un plano paralelo a la otra, de esta manera, el problema se reduce a determinar la distancia entre una recta en el espacio y un plano paralelo.
En la imagen izquierda puedes observar como la distancia entre las rectas M y R es el segmento AB perpendicular a un plano P, que contiene a la recta R, paralelo a la recta M.