1.1. Fundamentos
Recordemos que dos formas son proyectivas si una puede obtenerse de la otra mediante secciones y proyecciones.
La homología plana es una transformación homográfica generada por la proyección de un punto, siendo las dos figura homólogas secciones de dicha radiación.
Dos figuras homólogas se correspondan punto a punto y recta a recta respetando las siguientes leyes:
- Dos puntos homólogos (A y A') están alineados con un punto fijo (O) llamado centro de homología.
- Dos rectas homólogas se cortan en una recta llamada eje de homología.
En la siguiente animación te mostramos de manera detallada los fundamentos de la homología.
DT2 U2 T3 Apdo. 1.1: fundamentos de la homología
Video de Departamento DIBUJO IEDA alojado en Youtube
Coeficiente de homología.
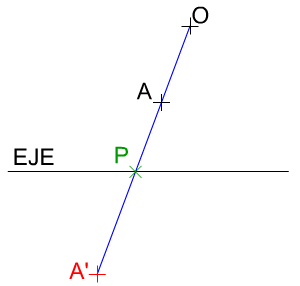En toda transformación se establece un coeficiente (k) o razón entre los elementos transformados.
En la homología este coeficiente es la razón doble que se establece entre un par de puntos homólogos (AA'), el centro de homología (O) y el punto intersección (P) de la recta que une dichos puntos (AA') con el eje.
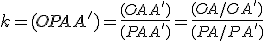
En la imagen de la izquierda puedes ver cómo se establece este coeficiente.
Objetivos
Teorema de Desargues.
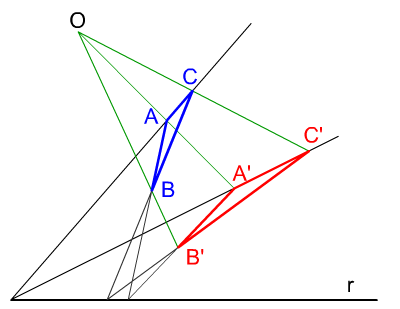En el plano proyectivo, dos triángulos son perspectivos desde un punto si y sólo si son perspectivos desde una recta.
En la imagen de la izquierda tienes una demostración de este teorema:
Dados los triángulos homólogos ABC y A'B'C' sus lados AD, BE y CF concurren en un mismo punto O. Así mismo, los pares de lados (AB, DE), (BC, EF) y (AC, DF) se cortan respectivamente sobre una misma recta r.
Pregunta Verdadero-Falso
Retroalimentación
Falso
Una recta homóloga solamente puede ser paralela al eje de homología si y solo si su origen es paralela a dicho eje.