3.1. Cónicas
Las superficies cónicas se caracterizan por tener un punto, llamado vértice, situado en el eje en el que se apoyan la recta que genera la superficie.
Dependiendo de la forma dela base pueden ser:
- Conos, la base o directriz es una circunferencia o una elipse.
- Pirámides, la base o directriz es un polígono, regular o irregular.
En la imagen superior te mostramos un cono recto de revolución representado según sus vistas diédricas, en perspectiva isométrica y su desarrollo.
Nota
Nosotros solamente vamos a estudiar los conos rectos de revolución y las pirámides regulares.
Representación diédrica del cono recto de revolución.
Cono apoyado en un plano que pasa por la LT.
Como la base es una circunferencia contenida en un plano oblicuo respecto de los de proyección, sus proyecciones diédricas serán elipses.
En este caso particular mediante una vista auxiliar de perfil podemos obtener la verdadera magnitud de la altura y la posición del vértice.
En la animación inferior te mostramos el procedimiento a seguir para trazar las proyecciones del cono recto de revolución apoyado en un plano que pasa por la LT.
DT2 U4 T1 Apdo. 3.1: cono apoyado plano pasa por la linea de tierra
Video de Departamento DIBUJO IEDA alojado en Youtube
Cono recto apoyado en un plano paralelo a la linea de tierra.
Sistema Diédrico. Cono recto apoyado en un plano paralelo a la Línea de Tierra
Video de Dpto. Dibujo Sierra de Aras alojado en Youtube
Pirámide apoyada en un plano proyectante vertical.
Para poder obtener las proyecciones diédricas de la base tenemos que abatir el plano proyectante, como es vertical (de canto) lo abatimos sobre el PHP, de esta manera los trazados auxiliares no interfieren en el resultado final.
La altura de la pirámide viene representada en verdadera magnitud en su proyección vertical ya que se trata de una recta frontal.
En la siguiente animación puedes ver cómo se determinan las proyecciones diédricas de una pirámide regular apoyada en un plano de canto.
DT2 U4 T1 Apdo. 3.1: pirámide apoyada en un plano proyectante vertical
Video de Departamento DIBUJO IEDA alojado en Youtube
Pirámide de base hexagonal apoya en un plano oblicuo.
PAU #010 Diédrico: Pirámide hexagonal (Dibujo Técnico Selectividad - Canarias/2000)
Video de PDD Profesor de Dibujo alojado en Youtube
Objetivos
Para dibujar la perspectiva de una pirámide primero tenemos que situar los vértices de la base y luego el vértice.
En el vídeo inferior puedes ver el método empleado en el trazado de la perspectiva caballera de una pirámide recta de base triangular, observa cómo se ha determinado la posición de cada punto según sus coordenadas.
REPRESENTACIÓN EN EL SISTEMA DIÉDRICO DE UNA PIRÁMIDE EN EL PRIMER CUADRANTE.
Video de JESUS DIAZ-MASA ZUAZO alojado en Youtube
Caso de estudio
|
|
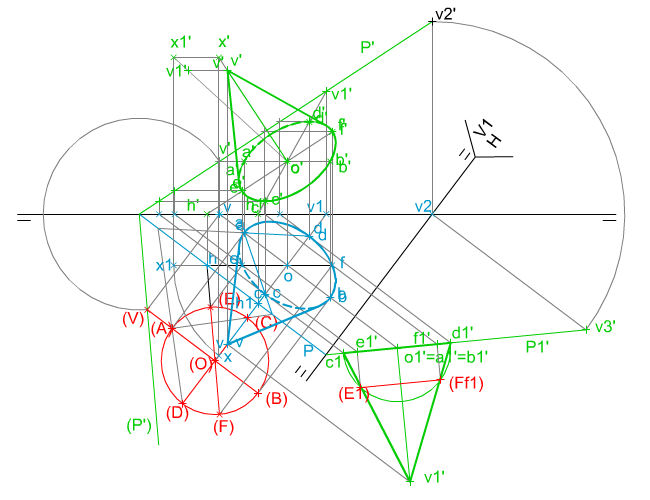
| En la imagen superior te mostramos cómo se han determinado las proyecciones diédricas de un cono recto de revolución apoyado en un plano oblicuo, conocido el centro y el radio de la base y su altura.
Observa cómo este ejercicio se ha resulto empleando dos procedimientos: mediante el abatimiento y aplicando un cambio de plano. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las herramientas de dibujo tradicionales. |
| Para realizar este ejercicio debes descargar este documento pdf. |