2.1. Triangulación
ROMBOIDE
Relación entre mediana y diagonal.
Como las diagonales de un romboide no tienen la misma longitud, este siempre quedará divido en dos o cuatro triángulos escalenos. Aplicando las propiedades aprendidas en el apartado anterior podemos establecer nuevas relaciones entre los lados y diagonales de este paralelogramo
En la siguiente animación puedes ver las relaciones que se establecen entre estos triángulos, ya sean sus ángulos, lados, medianas (diagonales) o alturas.
DT2 U1 T1 Apdo 2.1: Relaciones métricas del romboide
Video del Departamento de DIBUJO IEDA alojado en Youtube
TRAPECIOS.
Relación entre romboide y diagonales.
En el curso anterior estudiamos las propiedades de los trapecios, aplicándolas en su trazado.
En este apartado vamos a analizar la relación que existen entre las diagonales y cómo estas descomponen al cuadrilátero en un rombo y un triángulo, o en dos o cuatro triángulos. También estudiaremos la relación métrica que se establece entre la mediana del trapecio y sus diagonales.
En la siguiente animación puedes ver dichas relaciones.
DT2 U1 T1 Apdo 2.1: Relaciones métricas del trapecio
Video del Departamento de DIBUJO IEDA alojado en Youtube
Caso de estudio
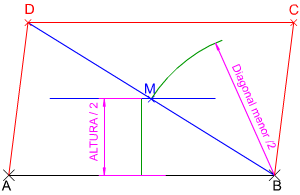
En la imagen izquierda tienes la construcción de un romboide conocido el lado mayor en verdadera posición y magnitud, la altura entre los lados mayores, y la longitud de la diagonal menor. En la resolución de este ejercicio hemos aplicado las relaciones métricas entre un romboide y un triángulo escaleno.
| ¿Quieres ver cómo se ha resuelto? |