1.1. Otra definición
Nota:
Te recomendamos que repases las definiciones de las curvas cónicas estudiadas en el tema anterior.
ELIPSE.
Es el lugar geométrico de todos los centros de las circunferencias que son tangentes a una circunferencia focal y que pasan por el otro foco.
En la animación inferior puedes ver cómo los puntos de una elipse (negro) son centros de circunferencias (rojo) tangentes a la focal (azul), lógicamente el punto de tangencia (verde) está alineado con el centro de la circunferencia tangente y el centro de la focal.
Está definición nos permitirá determinar, mediante potencia, el punto intersección de una recta con la elipse, pues cada uno de los centros de la circunferencias tangentes es el punto intersección de una recta con dicha curva, pasando la recta en este caso por el foco.
DT2 U2 T2 Apdo. 1.1: circunferencias tangentes a la focal en la elipse
Video de Departamento DIBUJO IEDA alojado en Youtube
HIPÉRBOLA.
Es el lugar geométrico de todos los centros de las circunferencias que son tangentes a una circunferencia focal y que pasan por el otro foco.
En la siguiente animación te mostramos cómo los puntos de una rama de una hipérbola (negro) son centros de circunferencias (rojo) tangentes a la focal (azul).
Es un caso similar al anterior, por tanto, podemos determinar, aplicando potencia, el punto intersección de una recta con la hipérbola, observa como la focal tangente es tangente interior a cada una de las circunferencia tangentes.
DT2 U2 T2 Apdo. 1.1: circunferencias tangentes a la focal en la hipérbola
Video de Departamento DIBUJO IEDA alojado en Youtube
PARÁBOLA.
Es el lugar geométrico de todos los centros de las circunferencias que son tangentes a la recta directriz y que pasan por el foco.
En la animación inferior puedes ver cómo el radio de cada una de las circunferencias tangentes es igual a la distancia tomada desde su centro al foco, esto nos recuerda la definición estudiada en el tema anterior: "..cualquiera de sus puntos equidista de una recta, llamada Directriz, y de un punto, llamado Foco".
Como en los casos anteriores, mediante potencia podemos determinar el punto intersección de una recta con la Parábola.
DT2 U2 T2 Apdo. 1.1: circunferencias tangentes a la directriz de una parábola
Video de Departamento DIBUJO IEDA alojado en Youtube
Caso de estudio
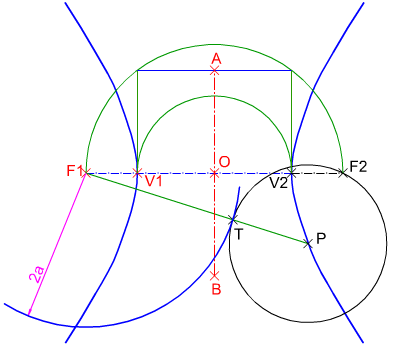En la figura de la izquierda puedes ver cómo se han determinado los ejes de simetría de una Hipérbola a partir de una circunferencia de centro P tangente en el punto T a la focal, uno de sus vértices (V2) y foco correspondiente (F2).
Para resolverlo debes repasar las nociones aprendidas sobre la Hipérbola en el tema anterior, y aplicar los conceptos y procedimientos explicados en este apartado.
Material necesario:
- Lápiz blando y duro.
- Compás.
- Plantilla de dibujo (escuadra y cartabón).
- Hojas para realizar trazados de prueba.
| Para realizar este ejercicio debes descargar este documento pdf. |