1.2. Tangencias, propiedades
Nota:
Para poder resolver problemas de tangencias antes debemos conocer sus propiedades, esto es, cómo se relacionan los elementos de cada una de las curvas cónicas con la recta tangente en cuestión.
ELIPSE.
En la siguiente animación puedes ver las relaciones que se establecen entre una recta tangente y la elipse, observa cómo podemos determinar algunos parámetros a partir de dichas relaciones.
DT2 U2 T2 Apdo. 1.2: recta tangente a la elipse y algunos parámetros
Video de Departamento DIBUJO IEDA alojado en Youtube
HIPÉRBOLA.
Como en el caso de la elipse, mediante las relaciones establecidas entre una recta tangente y una hipérbola podemos determinar parámetros de esta.
En la animación inferior puedes ver cómo se establecen dichas correspondencias.
DT2 U2 T2 Apdo. 1.2: recta tangente a la hipérbola y algunos parámetros
Video de Departamento DIBUJO IEDA alojado en Youtube
PARÁBOLA.
El caso de la parábola quizás es más singular ya que las relaciones que se establecen entre la recta tangente y esta curva tienen casi siempre un elemento en común la tangente principal.
En la siguiente animación puedes ver cómo en la primera, tercera, quinta y sexta propiedades están basadas en la recta tangente principal.
DT2 U2 T2 Apdo. 1.2: recta tangente a la parábola y algunos parámetros
Video de Departamento DIBUJO IEDA alojado en Youtube
Pregunta Verdadero-Falso
Retroalimentación
Verdadero
Caso de estudio
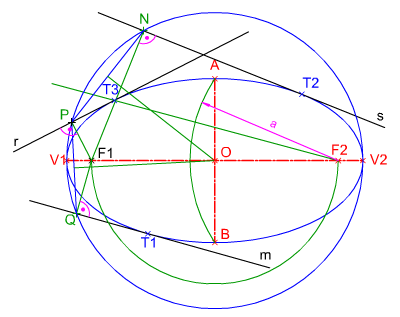En la figura de la izquierda puedes ver cómo se ha determinado los ejes de simetría de una Elipse a partir de uno de sus focos y tres rectas tangentes a dicha cónica.
Para resolverlo debes repasar las nociones aprendidas sobre la Elipse en el tema anterior, y aplicar los conceptos y procedimientos explicados en este apartado.
Material necesario:
- Lápiz blando y duro.
- Compás.
- Plantilla de dibujo (escuadra y cartabón).
- Hojas para realizar trazados de prueba.
| Para realizar este ejercicio debes descargar este documento pdf. |