1.2. Elipse
Definición.
La elipse es una curva cerrada y plana, cuyos puntos tiene la propiedad de que la suma de distancia de cada uno de ellos a otros dos fijos, llamados focos, es constante e igual al eje mayor de la elipse.
Los ejes se cortan perpendicularmente en el centro de la elipse, esta es simétrica respecto a los dos ejes.
El eje mayor se denomina eje real y el menor eje imaginario.
Observa cómo se puede construir una elipse a partir de una cuerda y entiende sus elementos:
Elementos.
Como comentamos en el apartado anterior no todas las curvas cónicas tienen los mismos elementos, en el caso de la Elipse sus elementos son todos los que podemos encontrar en una curva cónica, aunque alguno de ellos no sean esenciales para su determinación y trazado.
En la animación inferior puedes ver los elementos y propiedades de la Elipse:
DT2 U2 T1 Apdo. 1.1: elementos y parámetros de la elipse
Video del Departamento DIBUJO IEDA alojado en Youtube
Determinar los focos de una elipse.
Los focos de una Elipse se pueden determinar de distintas maneras, según los datos que nos den: dos ejes de simetría, el eje mayor y una recta tangente, etc.
En la animación inferior te mostramos cómo determinar los focos de una elipse a partir de los dos ejes de simetría.
DT2 U2 T1 Apdo. 1.2: determinar los foco de la elipse
Video del Departamento DIBUJO IEDA alojado en Youtube
Objetivos
Distancia de un punto a un foco.
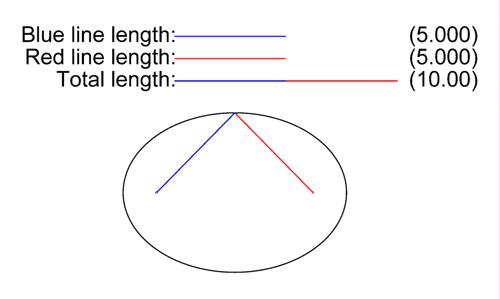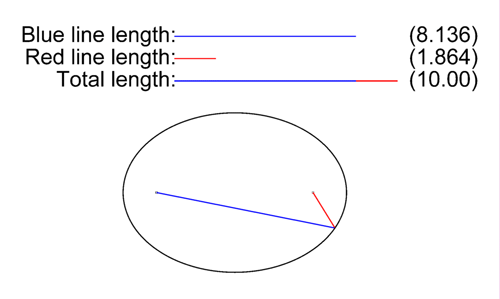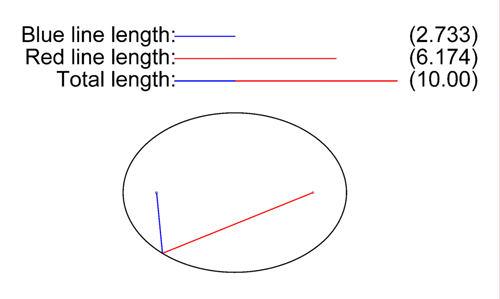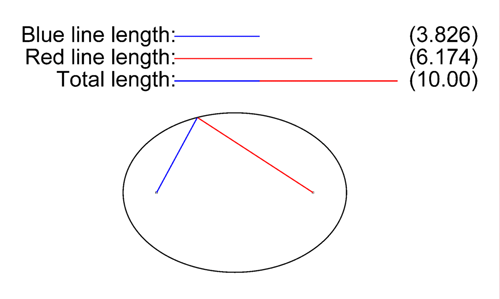
La distancia de un punto de una elipse a un foco de la dicha curva cónica viene determinada por el segmento vector que une ambos puntos.
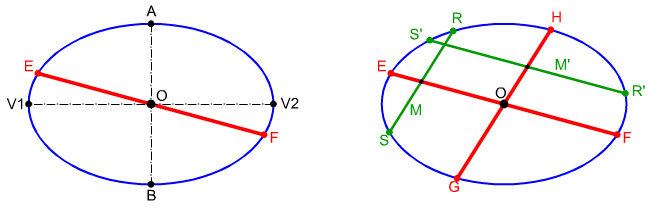
En la imagen de la izquierda (archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia) puedes ver cómo los vectores representados en colores cambian de tamaño reflejándose su magnitud real y la proporción de ambos sectores respecto del eje de simetría mayor.
En la imagen inferior puedes ver cómo el diámetro EF divide por la mitad en MA la cuerda RS paralela al diámetro GH y el diámetro hg divide por la mitad en M'A la cuerda R'S' paralela al diámetro EF, por tanto, ambos diámetros son conjugados.
Comprobar radios vectores.
Recordemos que un radio vector es el segmento que une cualquier punto de la curva con su foco correspondiente.
En la siguiente animación puedes comprobar los radios vectores de dos puntos X e Y de una Elipse.
DT2 U2 T1 Apdo 1.2: radios vectores de la elipse
Video del Departamento DIBUJO IEDA alojado en Youtube
Determinar los ejes de una elipse dada.
Geom plana, curvas cónicas, determinación de los ejes de una elipse dada su curva elíptica
Video de Juan Escobar alojado en Youtube
Pregunta Verdadero-Falso
Retroalimentación
Falso
La suma de las distancias de un punto de la curva respecto de los focos de la misma es igual al eje de simetría mayor (2a)Retroalimentación
Falso
El radio de la Circunferencia Focal es igual a la magnitud del eje de simetría mayor (2a).Caso de estudio
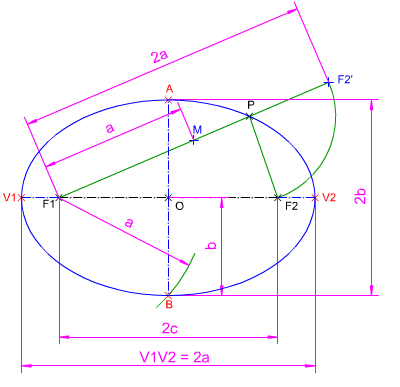 |
En la figura de la izquierda puedes ver cómo se han determinado los parámetros de una Elipse, dados su centro, los dos focos y un punto de la curva. Para resolverlo debes de aplicar los conceptos y procedimientos explicados en este apartado. Material necesario:
|
| Para realizar este ejercicio debes descargar este documento pdf. |