1.4. Parábola
Definición.
La parábola es una curva abierta y plana de una sola rama, de manera que cualquiera de sus puntos equidista de una recta, llamada Directriz, y de un punto, llamado Foco (F).
En la animación inferior puedes ver cómo el punto de la parábola siempre tiene la misma longitud respecto del foco y de la directriz:
Elementos.
Todos los elementos de las curvas cónicas que hemos estudiado hasta ahora no se dan en la Parábola. Al tener un solo eje de simetría posee solamente un Foco, y lógicamente no tiene circunferencia principal ni focal, esta carencia la sustituye la directriz, elemento esencial de este tipo de curva cónica.
En el video inferior puedes ver los elementos y propiedades de la Parábola:
Determinar elementos.
Para poder determinar los elementos y el parámetro de una Párabola necesitaremos como mínimo tres datos.
- La Directriz y el vértice. En la siguiente animación te mostramos cómo determinar estos elementos a partir de los siguientes datos: el eje, el foco y un punto de la curva.
DT2 U2 T1 Apdo. 1.4: determinar la directriz y el vértice de una parábola
Video del Departamento DIBUJO IEDA alojado en Youtube
- El eje, el foco y el vértice. En la siguiente animación te mostramos cómo determinar estos elementos a partir de los siguientes datos: la directriz y dos puntos de la curva.
DT2 U2 T1 Apdo. 1.4: determinar el eje, el foco y el vértice de la parábola
Video del Departamento DIBUJO IEDA alojado en Youtube
Objetivos
Radiotelescopio parabólico.

Los radiotelescopios, como las antenas de radar, concentran los haces de señales en un receptor situado en el foco, esto es posible gracias a que su diseño está basado en la parábola, recuerda que la distancia de un punto al foco es igual a la distancia paralela al eje hasta la directriz, por tanto, si situamos un emisor en el foco podremos enviar un haz de rayos paralelos al eje.
En la imagen superior (archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia) te mostramos dos vistas de un radiotelescopio en Raisting, Baviera (Alemania):
En el video inferior puedes ver, de manera esquemática, el funcionamiento de una antena parabólica, observa cómo todos los rayos al incidir sobre la superficie de la antena coinciden en un mismo punto, el foco de la parábola.
Caso de estudio
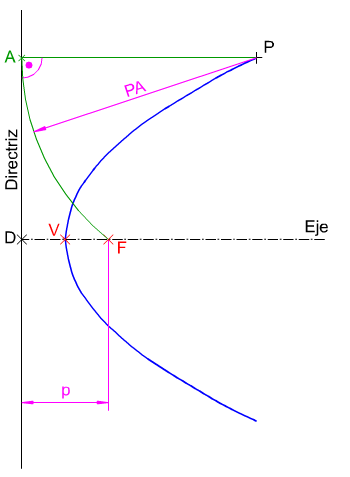
En la figura de la izquierda puedes ver cómo se ha determinado el parámetro de una Parábola, dados su eje de simetría, la directriz y un punto de la curva.
Para resolverlo debes de aplicar los conceptos y procedimientos explicados en este apartado.
Material necesario:
- Lápiz blando y duro.
- Compás.
- Plantilla de dibujo (escuadra y cartabón).
- Hojas para realizar trazados de prueba.
| Para realizar este ejercicio debes descargar este documento pdf. |