1.2. Tercera y cuarta proporcional
Importante
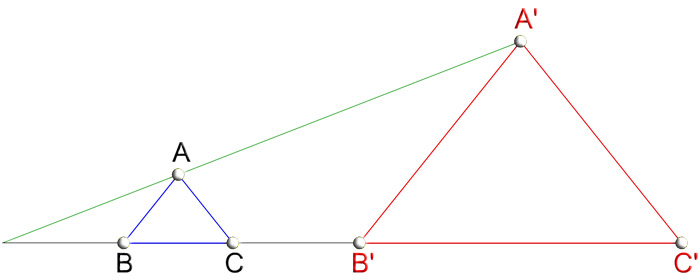
En geometría la proporción se da entre segmentos y para que estos queden perfectamente definidos usamos sus vértice, por tanto, esta transformación se dibuja usando la siguiente nomenclatura: los vértices los puntos proporcionales se representan en mayúscula (las letras), sin prima para los originales (A, B, C, 1, 2...). y con prima para los transformados (A', B', C', 1', 2'...).
DIVISIÓN DE UN SEGMENTO EN PARTES PROPORCIONALES: primero vamos a recordar cómo se dividía un segmento en partes iguales.
Dividir un segmento en partes iguales.
Video de PDD Profesor de Dibujo alojado en Youtube
Vídeo de Arturo Geometría alojado en Youtube
PROPORCIONALIDAD DE SEGMENTOS:
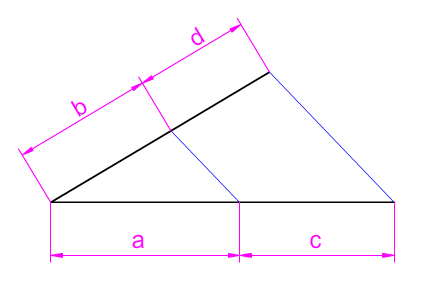
La razón entre dos segmentos es el valor de la relación entre las magnitudes de ambos segmentos, siendo a, b, c y d los términos de la proporción.
Cuando relacionamos dos razones establecemos una proporción (proporción es la igualdad de dos razones: a/b= c/d).
- A los términos a y d se les denomina extremos.
- A los términos b y c se les denominan medios.
- A los términos a y b se les denominan antecedentes.
- A los términos c y d se les denominan consecuentes.
TERCERA PROPORCIONAL:
Cuando dos de los términos conocidos (extremos o medios) tienen el mismo valor cualquiera de los otros recibirá el nombre de tercera proporcional. a/b = b/x.
Vídeo de PDD Profesor de Dibujo alojado en Youtube
CUARTA PROPORCIONAL:
Cuando se conocen tres de los cuatro términos, se puede obtener el cuarto, éste recibe el nombre de cuarta proporcional. a/b = c/x.
Vídeo de PDD Profesor de Dibujo alojado en Youtube