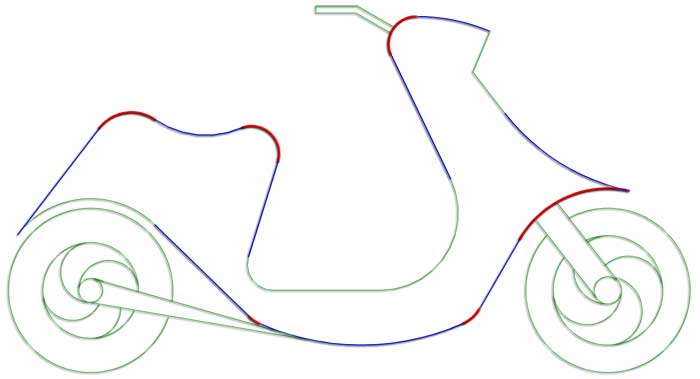
3.4. Enlaces de recta y circunferencia
Importante
Estos enlaces se resuelven aplicando el método de los lugares geométricos: paralelas y circunferencias concéntricas.
ENLACE DE UNA RECTA Y UNA CIRCUNFERENCIA.
- Dado el punto de enlace en la recta: hay dos posibilidades, que el arco de enlace sea exterior o que sea interior.
Arco de enlace exterior
Vídeo de Arturo Geometría alojado en Youtube
Arco de enlace interior
DT1 U2 T3 Apdo. 3.4: Enlace entre recta y circunferencia
Video del Departamento de DIBUJO IEDA alojado en Youtube
- Conocido el punto de enlace en la circunferencia: hay dos posibilidades, que el arco de enlace sea exterior o que sea interior.
Arco de enlace exterior
Vídeo de Arturo Geometría alojado en Youtube
Arco de enlace interior
DT1 U2 T3 Apdo. 3.4: Enlace entre recta y circunferencia 2
Video del Departamento de DIBUJO IEDA alojado en Youtube
- Conocido el radio de enlace: hay dos posibilidades, que el arco de enlace sea exterior o que sea interior.
Arco de enlace exterior
DT1 U2 T3 Apdo. 3.4: Enlace entre recta y circunferencia 3
Video del Departamento de DIBUJO IEDA alojado en Youtube
Arco de enlace interior
DT1 U2 T3 Apdo. 3.4: Enlace entre recta y circunferencia 4
Video del Departamento de DIBUJO IEDA alojado en Youtube
Curiosidad

Farola del Palacio Real de Aranjuez
Imagen de Ángel Serrano Sánchez de León en Wikimedia Commons. Licencia CC
Mediante enlaces no sólo se pueden unir distintos elementos, también se le puede dotar al diseño de todo el conjunto de cierta armonía y belleza.
En la imagen superior tienes un claro ejemplo en estas farolas de estilo Fernandino, en el Palacio Real de Aranjuez.
Caso práctico
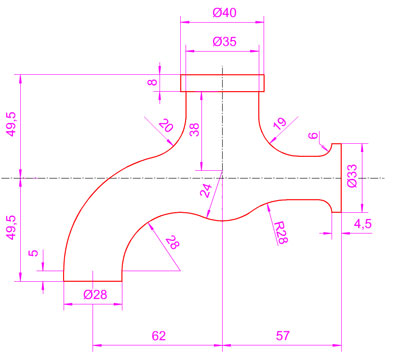
Dibuja la pieza representada en la imagen superior a escala 1/1 empleando los conceptos y procedimientos de las tangencias y enlaces entre rectas y circunferencias.
¿Necesitas ayuda para resolver este ejercicio?