2.1. Intersección
Los fundamentos de la intersección, así como los dos métodos que podemos emplear, los hemos analizado en el apartado anterior.
Ahora vamos a desarrollarlos de manera más detallada, aplicándolo en los poliedros ya estudiados.
En el vídeo superior puedes recordar cómo se determina la intersección entre una recta y un plano.
Importante
Cuando una recta intersecciona con un poliedro corta a las caras correspondientes que en realidad son planos.
Tetraedro, intersección con una recta horizontal.
Cuando una recta horizontal, o frontal, corta a un tetraedro determina de manera directa los puntos de intersección, ya que dicha recta estará contenida en un plano paralelo a uno de los de proyección.
En este caso particular determinaremos la intersección entre una recta horizontal y un tetraedro conteniendo dicha recta en un plano horizontal auxiliar.
DT2 U4 T2 Apdo. 2.1: intersección de recta horizontal con tetraedro
Video de Departamento DIBUJO IEDA alojado en Youtube
Tetraedro, intersección con una recta oblicua.
En el siguiente video puedes ver la intersección de una recta oblicua con un tetraedro. En el ejercicio se dan los datos de la proyección horizontal del tetraedro por lo que se comienza realizando el trazado para dibujar la proyección vertical. Está bien que repases este concepto. Es a partir del minuto 3:24 cuando se empieza a explicar el procedimiento a seguir para hallar la intersección de la recta dada con el tetraedro. Se emplea el método de plano proyectante por lo que la recta se va a contener en un plano proyectante horizontal. Si estás atento verás que es muy similar al anterior ejercicio "intersección del tetraedro con una recta horizontal". Por último, se halla la verdadera magnitud del trozo de recta que intersecciona a la superficie.
Conocimiento previo
En este video puedes ver en 3 dimensiones cómo se dibuja el tetraedro y la recta que la intersecciona. A su vez, podrás observar el plano proyectante auxiliar en el que la recta es contenida para hallar la intersección. Sería interesante que hicieras estos dibujos a la vez que vas estudiando el video. De esta forma tu capacidad de observación abstracta y tridimensional se irán desarrollando aún más.
Intersección de tetraedro con recta en sistema diédrico
Video de Néstor Martín Gulias alojado en Youtube
Hexaedro, intersección con una recta oblicua.
Como la recta oblicua corta a un hexaedro aplicaremos el segundo método estudiado en el primer apartado, así pues, contendremos la recta dada en un plano proyectante horizontal, determinando de manera directa los puntos intersección.
DT2 U4 T2 Apdo. 2.1: intersección de recta con un hexaedro
Video de Departamento DIBUJO IEDA alojado en Youtube
Octaedro, intersección con una recta oblicua.
En este último caso como la recta oblicua corta a un octaedro también aplicaremos el segundo método.
DT2 U4 T2 Apdo. 2.1: intersección de recta con un octaedro
Video de Departamento DIBUJO IEDA alojado en Youtube
Caso práctico
|
|
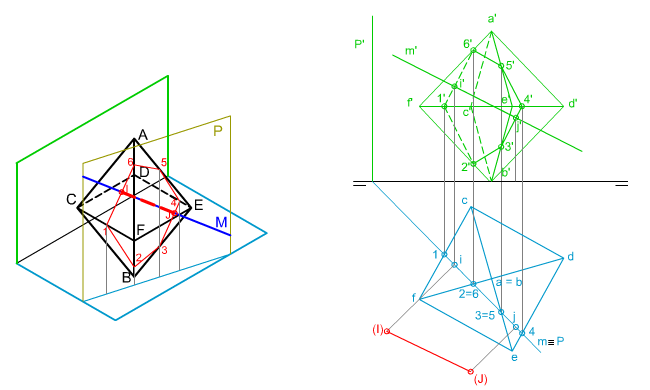
| En la imagen superior puedes ver cómo se ha determinado la verdadera magnitud del segmento intersección entre una recta dada M y un octaedro ABCDEF.
Conocemos las proyecciones diédricas de la recta y el poliedro. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para determinar la verdadera magnitud del segmento intersección IJ mediante las herramientas de dibujo tradicionales. |
| Para realizar este ejercicio debes descargar este documento pdf. |