3.1. Intersección
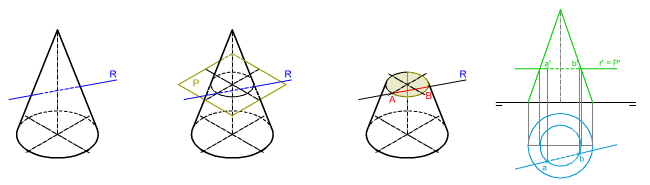
Como ocurre con los poliedros, una recta que no esté contenida en una superficie radiada solamente podrá tener en común con ella uno o dos puntos.
En el primer caso tocará a una generatriz o a una arista; y en el segundo cortará a dos generatrices, a dos caras, o a una cara y una arista.
En la imagen superior puedes ver cómo se ha determinado la intersección de una recta horizontal con un cono recto de revolución.
Importante
Para determinar la intersección de una recta con una pirámide o un prisma, aplicaremos los conceptos y procedimientos empleados con el tetraedro y hexaedro respectivamente.
Cono, intersección con una recta oblicua.
Para entender los pasos a seguir para este tipo de intersección es importante visualices este video. Una vez hayas asimilado lo que en él se explica observa la animación siguiente en la que se desarrolla el procedimiento para realizar la intersección.
Como la recta oblicua corta a un cono recto de revolución aplicaremos el primer método conteniendo la recta en un plano auxiliar, así pues, contendremos la recta dada en un plano oblicuo que pase por el vértice de dicho cono, lo que no simplificará bastante la determinación de los puntos intersección.
DT2 U4 T2 Apdo. 3.1: intersección de recta oblicua con un cono
Video de Departamento DIBUJO IEDA alojado en Youtube
Cono, intersección con una recta horizontal.
Si una recta horizontal, o frontal, corta a un cono los puntos de intersección no se determinan de forma directa; pero podemos simplificar el trazado si contenemos dicha recta en un plano paralelo a uno de los de proyección. Este es un caso particular por lo que debes estar atento al procedimiento a seguir para hallar la intersección. Repetimos, en este caso, el plano auxiliar no pasará por el vértice sino que será paralelo a uno de los planos de proyección.
En este caso particular determinaremos la intersección entre una recta horizontal y un cono recto de revolución conteniendo dicha recta en un plano horizontal auxiliar.
DT2 U4 T2 Apdo. 3.1: intersección de recta horizontal con un cono
Video de Departamento DIBUJO IEDA alojado en Youtube
Cilindro, intersección con una recta oblicua.
Como en el caso estudiado anteriormente en el hexaedro, si una recta oblicua corta a un cilindro aplicaremos el segundo método estudiado en el primer apartado, así pues, contendremos la recta dada en un plano proyectante horizontal, determinando de manera directa los puntos intersección.
DT2 U4 T2 Apdo. 3.1: intersección de recta oblicua con un cilindro
Video de Departamento DIBUJO IEDA alojado en Youtube
Objetivos
Aplicando las nociones aprendidas sobre la intersección entre recta y superficie radiadas podemos determinar cómo se seccionan dos superficies cilíndricas.
En el vídeo superior puedes ver de manera detallada, y en tres dimensiones, dicho procedimiento.
Caso de estudio
|
|
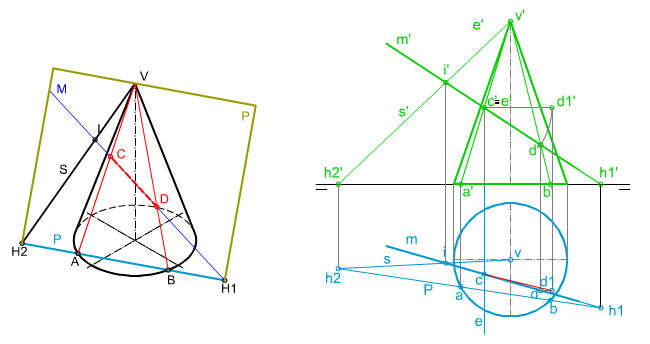
| En la imagen superior puedes ver cómo se ha determinado la verdadera magnitud del segmento intersección entre una recta dada M y un cono recto de revolución.
Conocemos las proyecciones diédricas de la recta y la superficie radiada. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para determinar la verdadera magnitud del segmento intersección CD mediante las herramientas de dibujo tradicionales. |
| Para realizar este ejercicio debes descargar este documento pdf. |